Ответы
Ответ дал:
0
Для 9 класса я бы сделал так:

Получаем совокупность двух уравнений:
Ответ:-4;-3;2.
Номер 23.
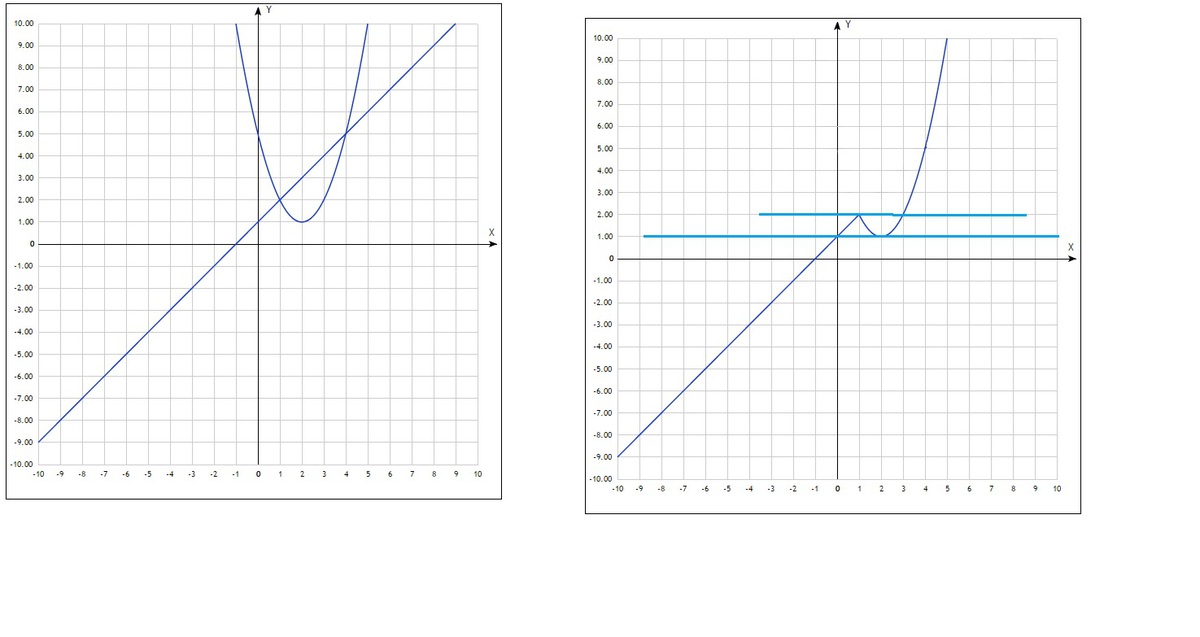
Можно сделать как: построить оба графика (Это 1-ая картинка), а потом стереть часть параболы, где x<1, у прямой стереть - где x>=1(Это 2-ая картинка).
Строить прямую по двум точкам, параболу: вершина
точки пересечения с осями: OY (0;5); OX - нет, т.к. дискриминант отрицательный, можно ещё пару точек (как хочешь).
Дальше по графику смотрим и видим, только при m=1 и m=2 будут две общие точки. Ответ: m=1, m=2.
Получаем совокупность двух уравнений:
Ответ:-4;-3;2.
Номер 23.
Можно сделать как: построить оба графика (Это 1-ая картинка), а потом стереть часть параболы, где x<1, у прямой стереть - где x>=1(Это 2-ая картинка).
Строить прямую по двум точкам, параболу: вершина
точки пересечения с осями: OY (0;5); OX - нет, т.к. дискриминант отрицательный, можно ещё пару точек (как хочешь).
Дальше по графику смотрим и видим, только при m=1 и m=2 будут две общие точки. Ответ: m=1, m=2.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад

