Найдите площадь трапеции, у которой параллельные стороны равны 10см и 15 см, а непараллельные - 7см и 4см.
Ответы
Ответ дал:
0
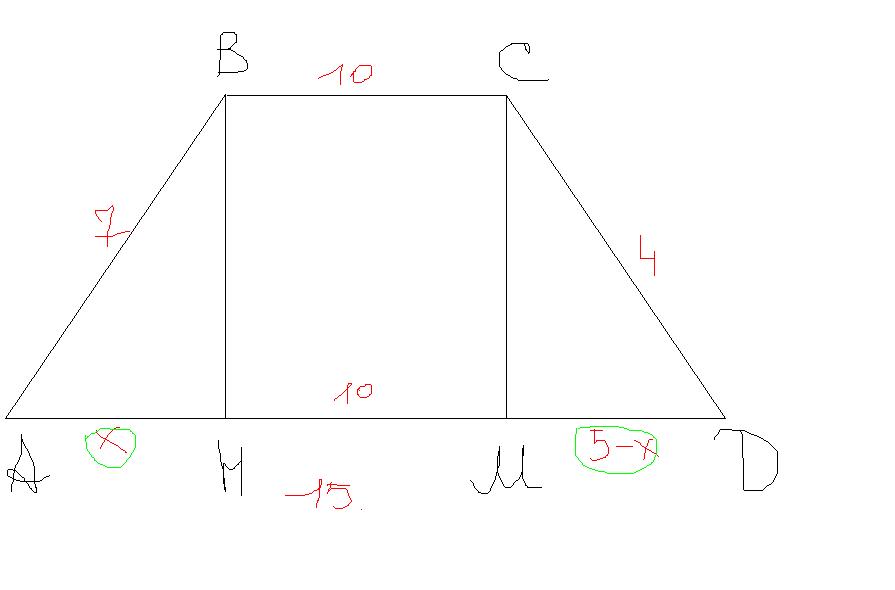
AH+MD=5 см
Из треугльника ABH прямоугольн. из теоремы Пифагора
Из треугольника MCD прямоугльн. из т. Пифагора
CM=BH=h, где h - высота трапеции
приравниваем
10x=58
x=5,8 см
отсюда S=72,5 см
Приложения:
Вас заинтересует
2 года назад
2 года назад
10 лет назад
11 лет назад