Question

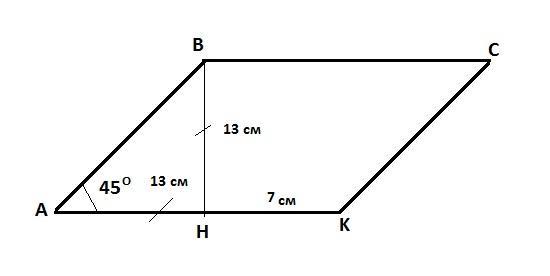
в параллелограмме abck высота bh разбивает сторону ak на отрезки ah = 13 см hk = 7 см а угол a = 45градусам найдите площадь параллелограмма

Answer 1

Ответ:

S = 260 см²

Объяснение:

Длина стороны AK:

AK = AH+HK = 13+7 = 20 см

Поскольку угол равен 45 градусам, то треугольник ABH - равнобедренный:

BH = AH = 13 см

Площадь:

S = AK·BH = 20·13 = 260 см²

Answer 2

Ответ:

260 см²

Объяснение:

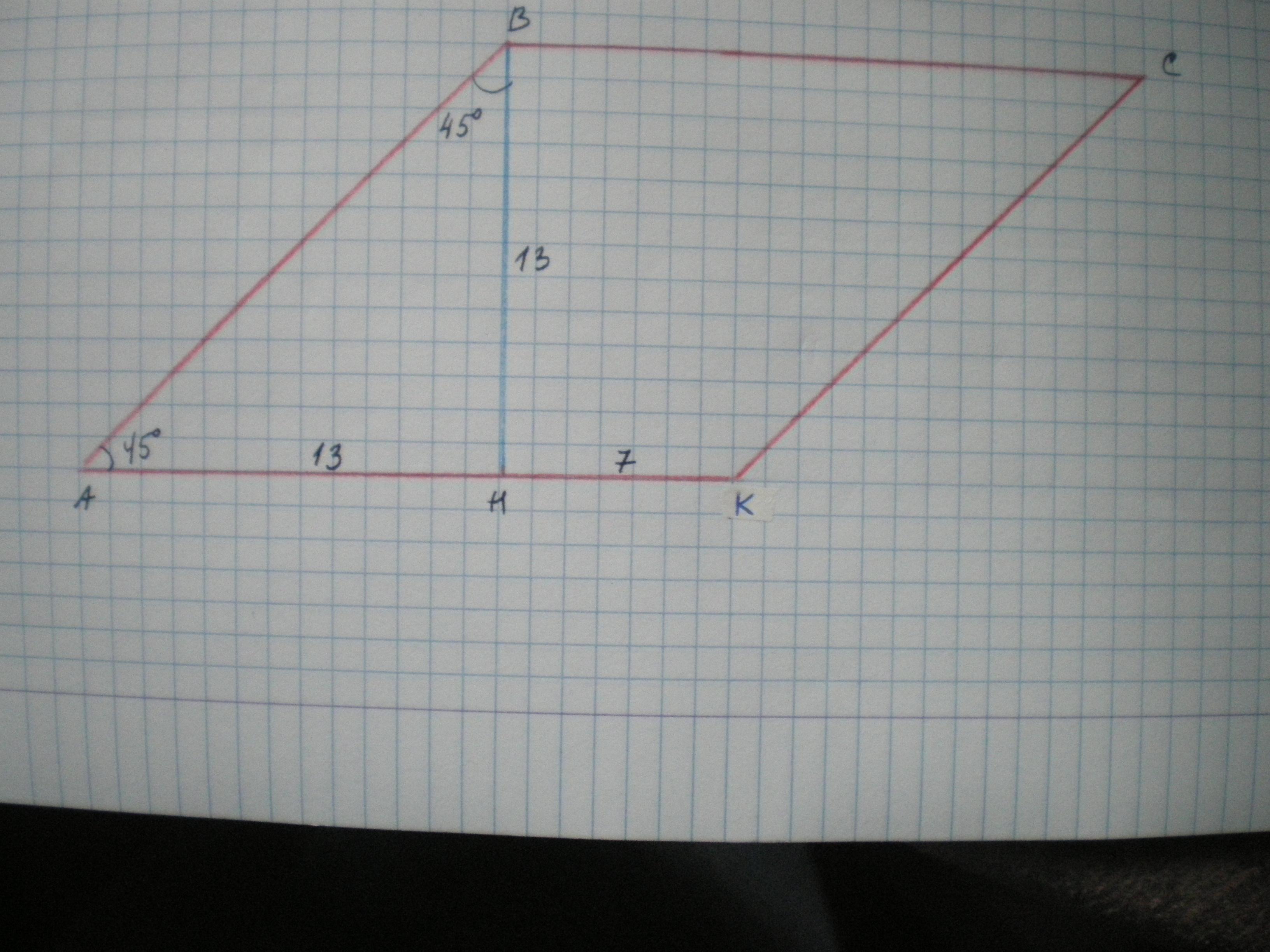
Дано: АВСК - параллелограмм, ВН - высота, АН=13 см, КН=7 см. ∠А=45°. Найти S(АВСК).

1) Рассмотрим ΔАВН - прямоугольный, ∠А=45°, ∠АВН=90-45=45°, значит, ΔАВН - равнобедренный и ВН=АН=13 см.

2) АК=АН+КН=13+7=20 см.

3) S(АВСК)=ВН*АК=13*20=260 см²