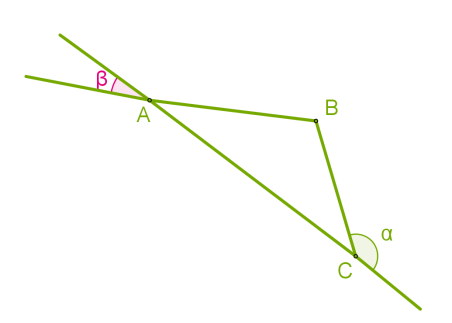
Точки A и C лежат на одной прямой, точка B не лежит на этой прямой, но находится в одинаковых расстояниях от точек A и C.
Величина угла∡α=152°.
Определи:
1. вид треугольника ABC — .
2. величину∡β=°.
Ответить!
Приложения:
Ответы
Ответ дал:
0
Так как расстояния ВА и ВС одинаковы, следовательно, треугольник равнобедренный. Углы α - внешний угол треугольника и в сумме с внутренним углом C, смежным с ним, составляет 180°. Следовательно, <C = 180°-152°=28°.
Углы при основании равнобедренного треугольника равны. Следовательно, <A=<C=28° a <B=180° - 2*28° = 124°. Треугольник АВС тупоугольный.
Углы β и <А вертикальные, следовательно, они равны.
Ответ: 1. Треугольник АВС тупоугольный, равнобедренный. 2 ∡β = 28°.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад