Question

ПОМОГИТЕ СРОЧНО
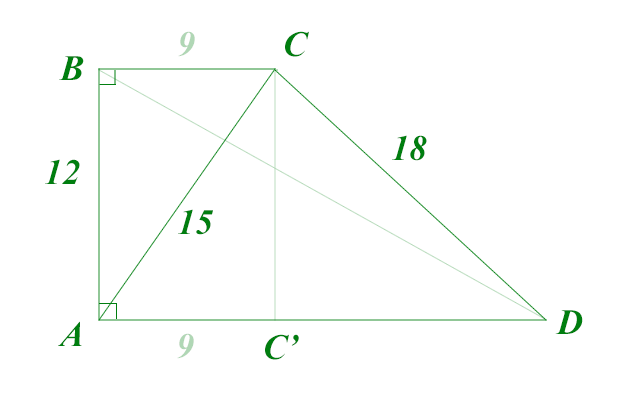
Трапеция ABCD – прямоугольная . Ее боковые стороны равны 12 см и 18 см, а диагональ АС равна 15 см. Найдите основания трапеции.

Answer 1

в прямоуг.треуг.АВС(<B=90) BC^2=AC^2-AB^2. BC^2=225-144=81. BC=9.
Проведем высоту СК,СК=АВ=12.
В прямоуг.треуг.СКД(<K=90) КД^2=CД^2-CK^2. KД ^2=324-144=180. КД=6V5.
АД=9+6V5

Answer 2

 Посмотрит как найти нужные математические символы   http://prntscr.com/73xb01   

Answer 3

Поскольку трапеция $ABCD$ прямоугольная, то значит одна из её сторон перпендикулярна основаниям, а другая – наклонная. При этом есть две диагонали: одна идёт из прямого угла в тупой к короткому основанию, а другая – из прямого в острый к длинному основанию. Та диагональ, которая идёт к длинному основанию лежит напротив тупого угла трапеции, а значит она длиннее и короткого основания, и длинной боковой стороны (см. чертёж). Отсюда ясно, что указанная диагональ $AC$ – может быть только диагональю идушей из прямого угла в тупой угол к короткому основанию. В соответствии с этим, расставим названия верщин трапеции $ABCD .$ Значит, $AB = 12$ см, а $CD = 18$ см.

$BC$ легко найти по теореме Пифагора:

$BC = sqrt{ AC^2 - AB^2 } = sqrt{ 15^2 - 12^2 }$ см = $sqrt{ 3^2 5^2 - 3^2 4^2 }$ см $=$

$= sqrt{ 3^2 ( 5^2 - 4^2 ) }$ см $= 3 sqrt{ 25 - 16 }$ см $= 3 sqrt{9}$ см $= 3 cdot 3$ см $= 9$ см ;


$AD = AC' + C'D = BC + C'D$ ;

$C'D$ легко найти по теореме Пифагора, учитывая, что $C'C = AB$ :

$C'D = sqrt{ CD^2 - C'C^2 } = sqrt{ CD^2 - AB^2 } = sqrt{ 18^2 - 12^2 }$ см $=$

$= sqrt{ 6^2 3^2 - 6^2 2^2 }$ см $= sqrt{ 6^2 ( 3^2 - 2^2 ) }$ см $= 6 sqrt{ 9 - 4 }$ см $= 6 sqrt{5}$ см ;

Итак: $AD = 9$ см $+ 6 sqrt{5}$ см ;


О т в е т : $BC = 9$ см ; $AD = ( 9 + 6 sqrt{5} )$ см .