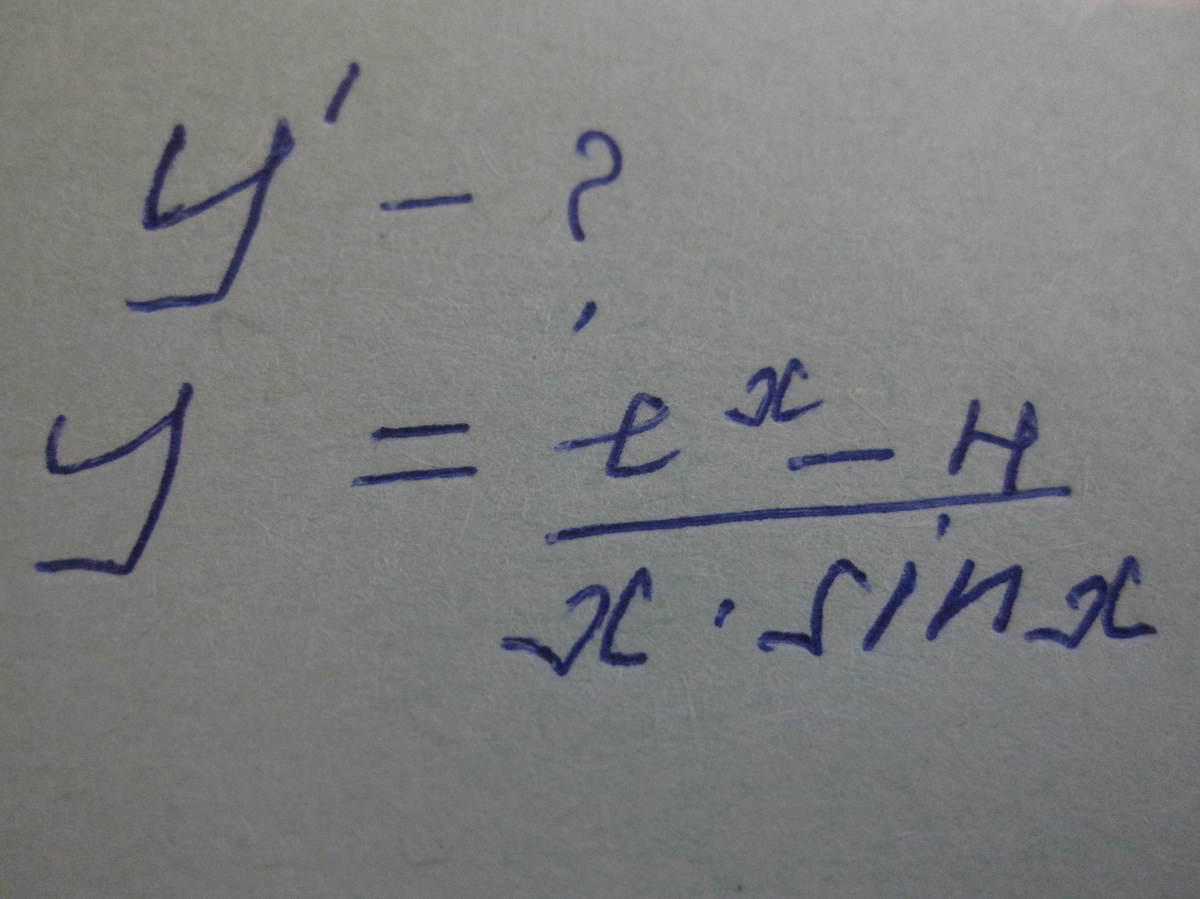Ответы
Ответ дал:
0
(u/v)'=(u'v-uv')/v^2
((e^x-4)/(x*sinx))'=((e^x-4)'(x*sinx)-(e^x-4)(x*sinx)')/(xsinx)^2=
=(e^x(x*sinx)-(e^x-4)(sinx+x*cosx))/(xsinx)^2
((e^x-4)/(x*sinx))'=((e^x-4)'(x*sinx)-(e^x-4)(x*sinx)')/(xsinx)^2=
=(e^x(x*sinx)-(e^x-4)(sinx+x*cosx))/(xsinx)^2
Ответ дал:
0
y'=((e^x-4)/(x*sinx))'=((e^x-4)' *(x*sinx)-(x*sinx)' * (e^x-4))/(x*sinx)²=
=(e^x*(x*sinx)-(e^x-4)*(x' *sinx+x*(sinx)'))/(x*sinx)²=
=(e^x*x*sinx-(e^x-4)*(sinx+x*cosx))/(x*sinx)²
=(e^x*(x*sinx)-(e^x-4)*(x' *sinx+x*(sinx)'))/(x*sinx)²=
=(e^x*x*sinx-(e^x-4)*(sinx+x*cosx))/(x*sinx)²
Ответ дал:
0
вместо второго e^x будет (e^x-4)
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад