Решите неравенство
Левую часть я преобразовала, сделала замену переменной, а что с правой частью делать, не знаю :с
Приложения:
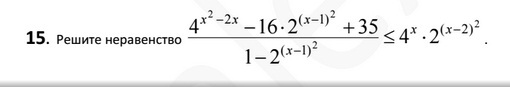
Ответы
Ответ дал:
0
Правая часть: 4^x*2^(x-2)²=2^(2*x)*2^(x²-4x+4)=2^(x²-4x+4+2x)=
=2^(x²-2x+4)=2^(x-2)².
=2^(x²-2x+4)=2^(x-2)².
Ответ дал:
0
числитель будет всегда положителен, потому как дискриминант соответствующего уравнения отрицательный. Тогда
то есть любое число кроме 1 есть решением этого неравенства
Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад