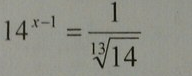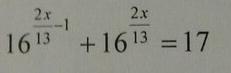Ответы
Ответ дал:
0
Ответ дал:
0
Нет... А зачем? - Там ведь нет квадратного уравнения..))
Ответ дал:
0
мы решали с буковкой t всегда через дискриминант, это способ такой
Ответ дал:
0
не всегда замена приводит к квадратному уравнению. Порой удобно заменить чтобы не писать громоздкие выражения.
Ответ дал:
0
всё же, спасибо!
Ответ дал:
0
Не за что..))) Обращайтесь!
Ответ дал:
0
1) 14^(х-1) = 14^(-1/13); х-1 = -1/13; х=1-1/13;
х = 12/13
2)

2x/13 = 1; 2х =13;
х = 6,5
х = 12/13
2)
2x/13 = 1; 2х =13;
х = 6,5
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад