из одной точки к окружности проведены касательная и секущая.Касательная длиннее внутренней и внешней частей секущей на 2 и 4 см.Найти длину секущей)))плииз
Ответы
Ответ дал:
21
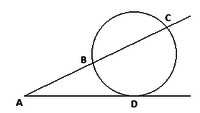
AB= AD-4
BC= AD-2
AC= AB+BC
AC= 2AD-6
Если из одной точки проведены к окружности касательная (AD) и секущая (AC), то произведение всей секущей на её внешнюю часть (AB) равно квадрату касательной.
AD^2 = AC·AB
AD^2 = (2AD-6)(AD-4)
---
AD=x
x^2 = (2x-6)(x-4) <=>
x^2 = 2x^2 -6x -8x +24 <=>
x^2 -14x +24 =0
x1= 2 (лишний, т.к. AD-2=BC, BC>0)
x2= 12
AD=12
---
AC= 2·12 -6 =18
BC= AD-2
AC= AB+BC
AC= 2AD-6
Если из одной точки проведены к окружности касательная (AD) и секущая (AC), то произведение всей секущей на её внешнюю часть (AB) равно квадрату касательной.
AD^2 = AC·AB
AD^2 = (2AD-6)(AD-4)
---
AD=x
x^2 = (2x-6)(x-4) <=>
x^2 = 2x^2 -6x -8x +24 <=>
x^2 -14x +24 =0
x1= 2 (лишний, т.к. AD-2=BC, BC>0)
x2= 12
AD=12
---
AC= 2·12 -6 =18
Приложения:
Вас заинтересует
1 год назад
2 года назад
7 лет назад
9 лет назад