Question

в равнобедренном треугольнике основание равно 40см, а боковая сторона 25 см, найдите тангенс угла при основании

Answer 1

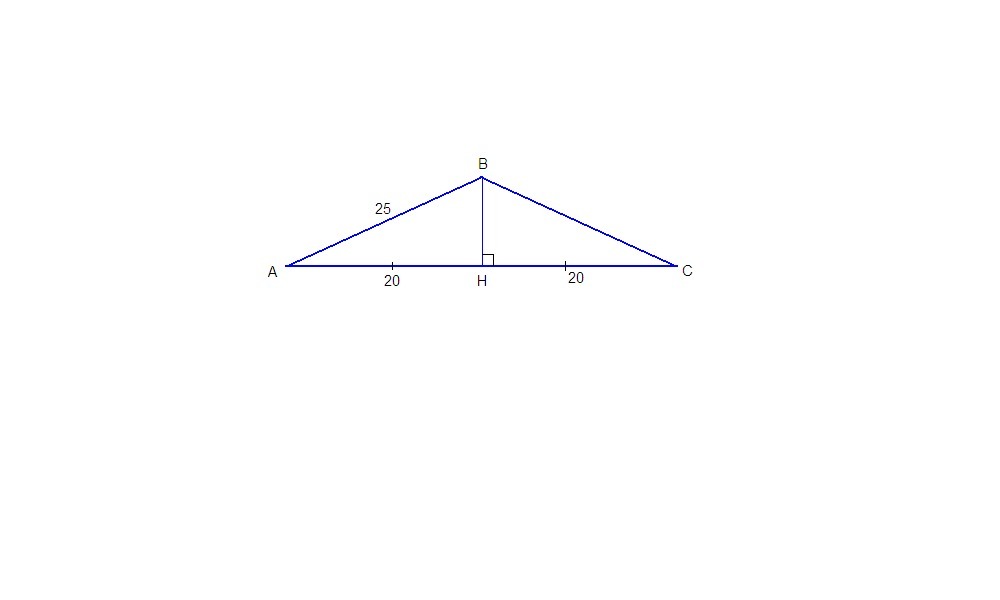
Пусть в ΔАВС АВ = ВС.
Проведем высоту ВН к основанию.
По свойству равнобедренного треугольника, высота является и медианой:
АН = НС = 40/2 = 20 см.
ΔАВН: ∠АНВ = 90°, по теореме Пифагора
             ВН = √(АВ² - АН²) = √(25² - 10²) = √((25 - 20)(25 + 20)) = √(5 · 45) = 5 · 3 = 15 см
             tg∠BAH = BH / AH
              tg∠BAH = 15 / 20 = 3/4 = 0,75