Question

Вероятности успешной сдачи экзамена по первому, второму и третьему
предмету у данного студента равны 0,6; 0,7; 0,8. Найти вероятность того, что он: а) сдаст
все экзамены; б) не сдаст хотя бы один экзамен; в) сдаст только первый экзамен

Answer 1

Вероятности
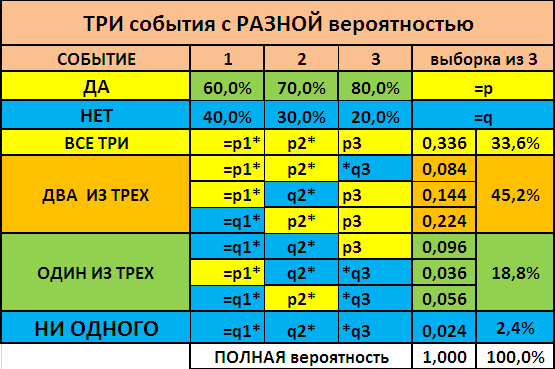
СДАТЬ даны  p(i) = 0,6 и 0,7 и 0,8,
НЕ СДАТЬ = q(i)= 1-р(i) = 0.4 и 0,3 и 0,2.
Задача а)
Сдать ТРИ экзамена - вероятности умножаются
Р(А) = p1*p2*p3 =0.6*0.7*0.8 = 0.336 = 33.6%
Задача б)
Не сдать хотя бы один - ДВА сдать и один - НЕТ.
Складываем вероятности событий
Р(Б) =p1*p2*q3+p1*q2*p3 + q1*p2*p3 = 0.084+0.144+0.224 = 0.452 = 45.2%
Задача в)
Сдать только первый - ДАНО = р(1)=0,6 = 60%.
СПРАВОЧНО: Эти и другие варианты сведены в таблицу.