Ответы
Ответ дал:
0
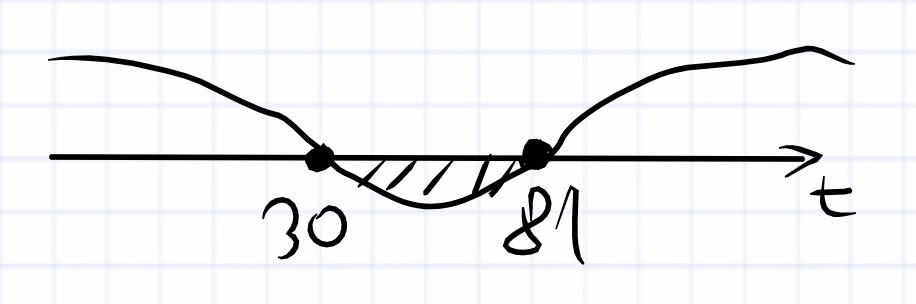
Найдём нули функции
Отметим нули функции на координатной прямой и выясним знаки функции на интервалах (рисунок прилагается).
t ∈ [30;81];
Ответ: х∈
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад