Question

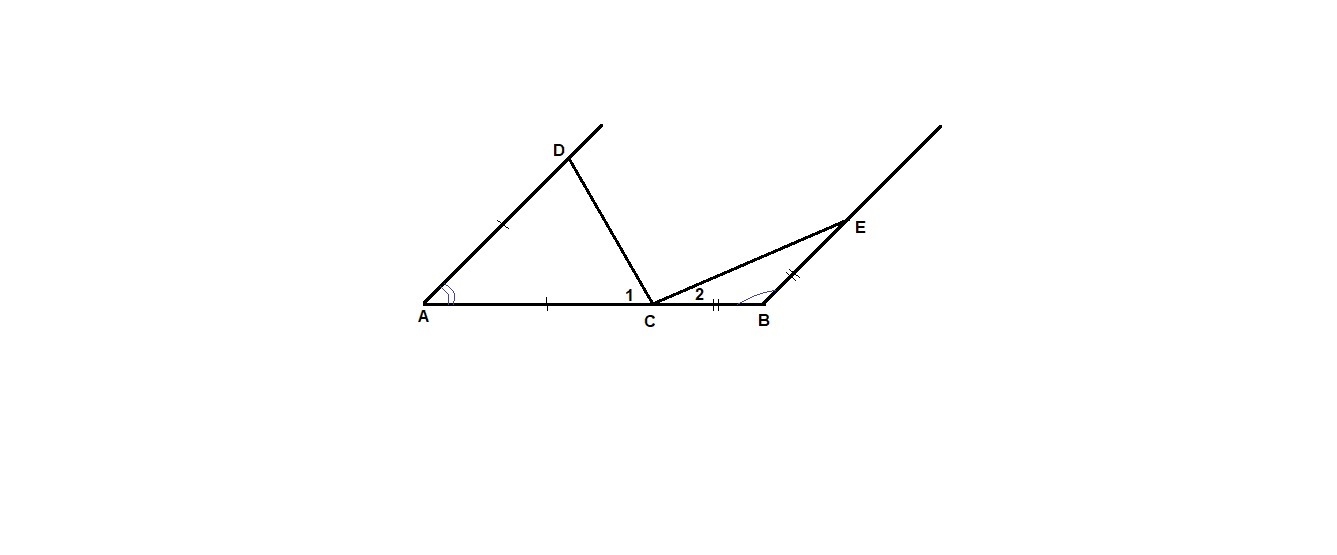
На отрезке АВ взята точка С. Через точки А и В проведены по одну сторону от АВ параллельные лучи. На них отложены отрезки АД=АС и ВЕ=ВС. Точка С соединена отрезками прямых с точками Д и Е. Докажите, что ДС перпендикулярно СЕ

Доказать с помощью параллельности прямых, желательно

Answer 1

∠ADC = ∠ACD = ∠1, так как ΔADC равнобедренный, тогда

∠DAC = 180° - 2· ∠1

∠ВСЕ = ∠ВЕС = ∠2, так как ΔВАС равнобедренный, тогда

∠ЕВС = 180° - 2 · ∠2

∠DAC + ∠EBC = 180° как внутренние односторонние углы при пересечении параллельных прямых AD и ВЕ секущей АВ.

180° - 2 · ∠1 + 180° - 2 · ∠2 = 180°

360° - 2(∠1 + ∠2) = 180°

2(∠1 + ∠2) = 180°

∠1 + ∠2 = 90°

∠DCE = 180° - (∠1 + ∠2) = 180° - 90° = 90°, значит

DC⊥CE