Найдите высоту цилиндра , диагональ осевого сечения и радиус основания которого равны соответсвенно 17 и 4
Ответы
Ответ дал:
0
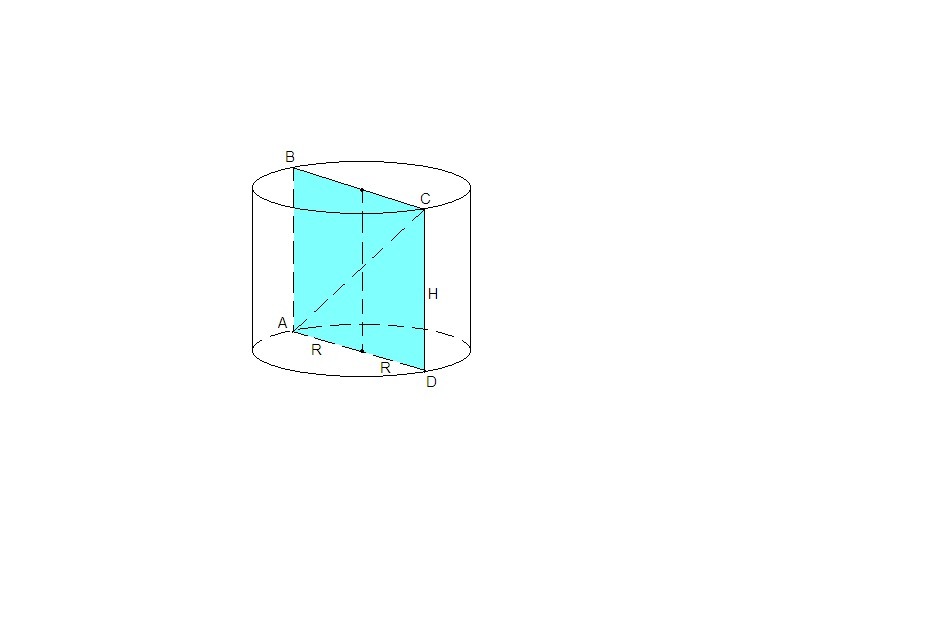
Осевое сечение цилиндра - прямоугольник, одна сторона которого равна высоте, а другая - диаметру основания.
AD = 2R = 8,
ΔACD: ∠ADC = 90°, по теореме Пифагора
CD = √(AC² - AD²) = √(17² - 8²) = √(289 - 64) = √225 = 15
H = 15
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад