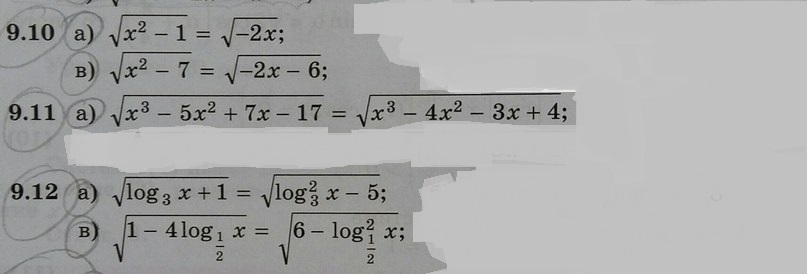Question

решите уравнения пожалуйста.........

Answer 1

$9.10a) sqrt{x^2-1}=sqrt{-2x}\x^2-1geq0;(x+1)(x-1)geq0\-2xgeq0;xleq0\D(f)in(-inf;-1)\x^2-1=-2x\x^2+2x-1\D=4+4=8\x_1=frac{-2+2sqrt2}{2}=sqrt2-1\x_2=frac{-sqrt2-1}{2}=-sqrt2-1$

первый корень уж точно не принадлежит области определения, поэтому его рассматривать не станем.

Наверное, и без помощи калькулятора всякий уважающий себя человек знает, что √2 ≈ 1,41. так вот -√2-1 ≈ -2,41, и он входит в D(f). Следовательно, он и является ответом.

$sqrt{x^2-7}= sqrt{-2x-6}\ left {{{x^2-7geq0;(x-sqrt7)(x+sqrt7)geq0}atop {-2x-6geq0};xleq0}right.\\D(f)in(-inf;-sqrt7][sqrt7;3]\\x^2-7x=-2x-6\x^2+2x-1$

вышла аналогичная ситуация. теперь нам необходимо только проверить, входят ли корни в D(f)

Первый корень = √2-1≈0,414
Второй корень = -√2-1≈-2,414

Для того чтобы убедиться,нужно сверить их квадраты.

(√7)² = 7
(-√2-1)² = 2 +2√2+1 = 3+2√2 ≈ 5.83.
(√2-1)²= 2 - 2√2 +1 = 3 - 2√2 ≈0.17

Ни один из корней, даже будучи с отрицательным знаком, не входит D(f)