Отрезок AD - биссектриса треугольника ABC. Через точку D проведена прямая, пересекающая сторону AB в точку Е так, что АЕ=ED. Найдите углы треугольника
AED, если угол ВАС= 64 градуса. Плииз срочно
Ответы
Ответ дал:
0
Т.к. АD - биссектриса, то ∠CAD=∠EAD=∠BAC : 2 = 64° : 2 = 32°.
Рассмотрим ΔAED. Так как АЕ=ЕD, то он равнобедренный с основанием AD. У равнобедренного треугольника углы при основании равны => ∠EAD=∠EDA=32°.
Сумма углов треугольника равна 180°. Значит, ∠EAD+∠EDA+∠AED=180°.
Отсюда ∠AED=180°-∠EAD-∠EDA=180°-32°-32°=116°.
Рассмотрим ΔAED. Так как АЕ=ЕD, то он равнобедренный с основанием AD. У равнобедренного треугольника углы при основании равны => ∠EAD=∠EDA=32°.
Сумма углов треугольника равна 180°. Значит, ∠EAD+∠EDA+∠AED=180°.
Отсюда ∠AED=180°-∠EAD-∠EDA=180°-32°-32°=116°.
Приложения:
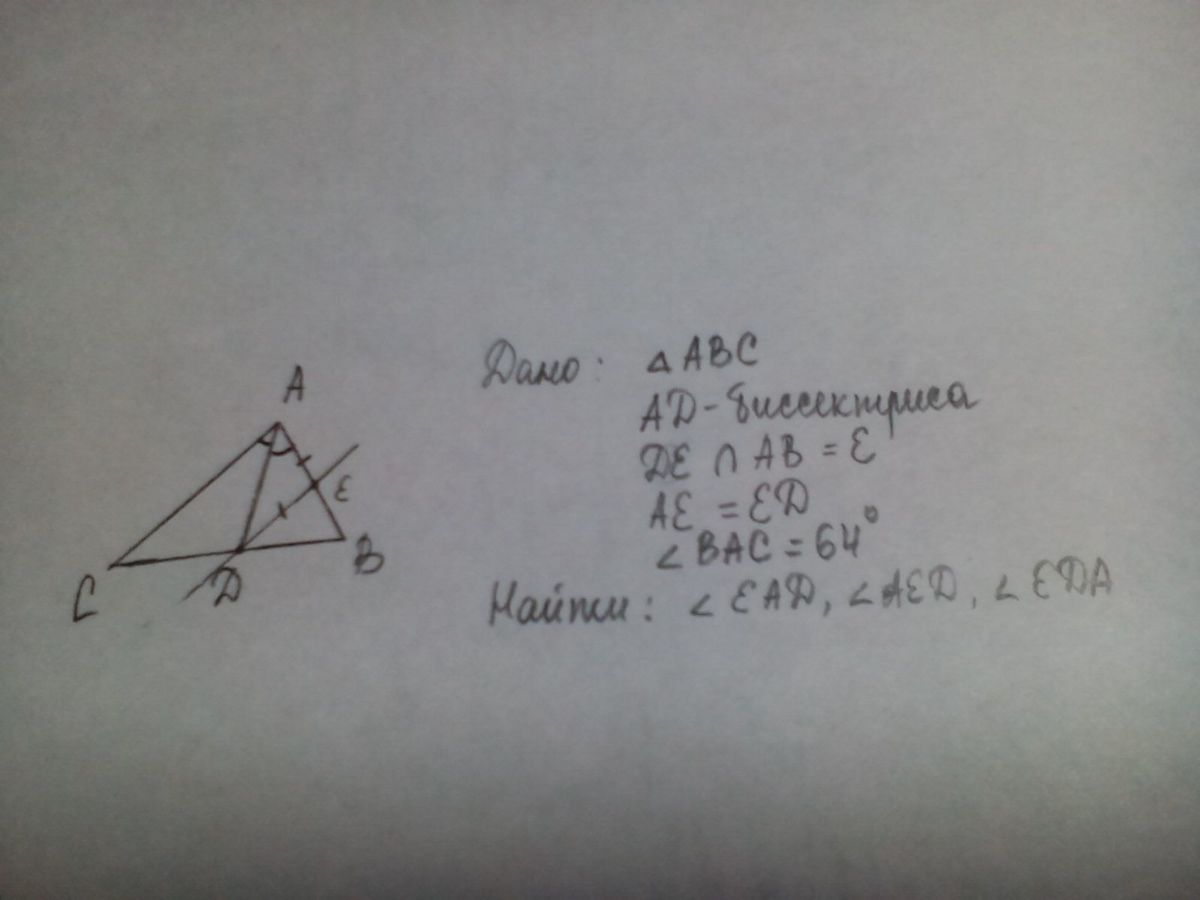
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад