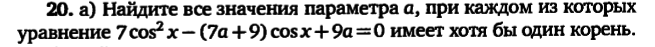Ответы
Ответ дал:
0
При каких значениях параметра а уравнение имеет хотя бы один корень
7 -(7a+9)cosx+9a=0
-(7a+9)cosx+9a=0
Пусть cosx=y, ,
,
7 -(7a+9)y+9a=0
-(7a+9)y+9a=0
D= -7*4*9a=49
-7*4*9a=49 +126a+81-252a=49
+126a+81-252a=49 -126a+81=
-126a+81= , при любых значениях параметра а дискриминант квадратного уравнения не принимает отрицательные значения, т.е. уравнение может иметь корни (
, при любых значениях параметра а дискриминант квадратного уравнения не принимает отрицательные значения, т.е. уравнение может иметь корни ( =
= =I7a-9I)
=I7a-9I)
y= или y=
или y=
при a<1 I7a-9I= - (7a-9)
I7a-9I= - (7a-9)
Получаем корни
y= или y=
или y=
y= y=a
y=a
уравнение не имеет корней, при
т.к. уравнение имеет хотя бы 1 корень
уравнение имеет хотя бы 1 корень
при a
 I7a-9I=7a-9
I7a-9I=7a-9
y=
или y=
данные значения а не удовлетворяет условию
ответ: при а∈[-1, 1]
7
Пусть cosx=y,
7
D=
y=
при a<1
Получаем корни
y=
y=
уравнение не имеет корней, при
т.к.
при a
y=
или y=
данные значения а не удовлетворяет условию
ответ: при а∈[-1, 1]
Ответ дал:
0
Т.е. ответ (-беск; 1 2/7)??
Ответ дал:
0
Все, понятно
Ответ дал:
0
если не трудно, можно отметить решение как лучшее
Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад