Question

исследование функции y=(x^2)/(x^2-1)

Answer 1

1. Область определения функции: $x^2-1ne 0;,,,,, Rightarrow,, xne pm 1$
$D(f)=(-infty;-1)cup(-1;1)cup(1;+infty)$
2. Исследуем на четность.
$y(-x)= dfrac{(-x)^2}{(-x)^2-1} = dfrac{x^2}{x^2-1}=y(x)$
Поскольку $y(-x)=y(x)$, то эта функция четная.

3. Функция не периодическая.
4. Точки пересечения с осью Ох и Оу.
   4.1. С осью Ох (если у=0)
$dfrac{x^2}{x^2-1} =0;,,,,,,Rightarrow,,,, x^2=0;,,,,,,,, Rightarrow,,,,, x=0$
  4.2. C осью Оу (если х = 0)
$y=0$

5. Точки экстремумы и монотонность функции:
$y'= dfrac{(x^2)'(x^2-1)-x^2(x^2-1)'}{(x^2-1)^2} =- dfrac{2x}{(x^2-1)^2}$
Приравниваем производную функции к нулю:
$- dfrac{2x}{(x^2-1)^2}=0;,,,,,,, Rightarrow,,,,,, x=0$

__+___(-1)__+___(0)___-___(1)___-____
Функция возрастает на промежутке $x in (-infty;-1)$ и $x in (-1;0)$, а убывает на промежутке $x in (0;1)$ и $xin (1;+infty)$
В окрестности точки $x=0$ производная функции меняет знак с (+) на (-), следовательно, точка $x=0$ - точка максимума.

5. Точки перегиба.
Вычисляем вторую производную функции:
$bigg(- dfrac{2x}{(x^2-1)^2}bigg)'=- dfrac{(2x)'(x^2-1)^2-2x((x^2-1)^2)'}{(x^2-1)^4} =\ \ \ =- dfrac{2(x^2-1)^2-2xcdot 2(x^2-1)}{(x^2-1)^4} = dfrac{2(3x^2+1)}{(x^2-1)^3}$

Приравниваем к нулю
$dfrac{2(3x^2+1)}{(x^2-1)^3} =0\ \ 3x^2+1=0$
Уравнение решений не имеет, так как левая часть уравнения принимает только положительные значения.

___+____(-1)___-____(1)___+___
На промежутке $x in (-infty;-1)$ и $x in (1;+infty)$ функция вогнута, а на промежутке $x in (-1;1)$ функция выпукла.

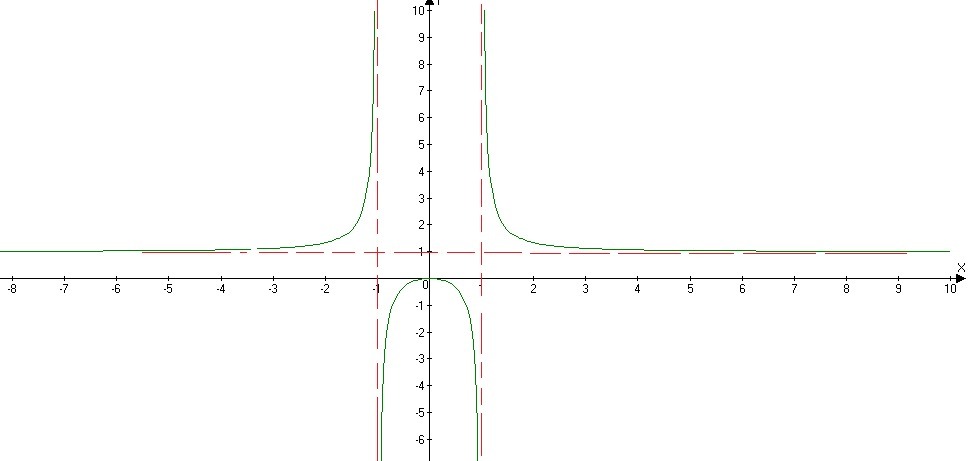
Вертикальные асимптоты: $x=pm1$

Горизонтальные асимптоты: 
  $displaystyle dfrac{x^2}{x^2-1} = dfrac{x^2pm1}{x^2-1} =1+ frac{1}{x^2-1} to_{nto infty}1$
$y=1$ - горизонтальная асимтота

Наклонных асимптот нет.