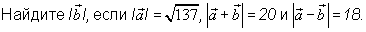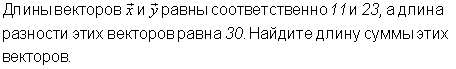Ответы
Ответ дал:
0
Второй решается аналогично
Приложения:
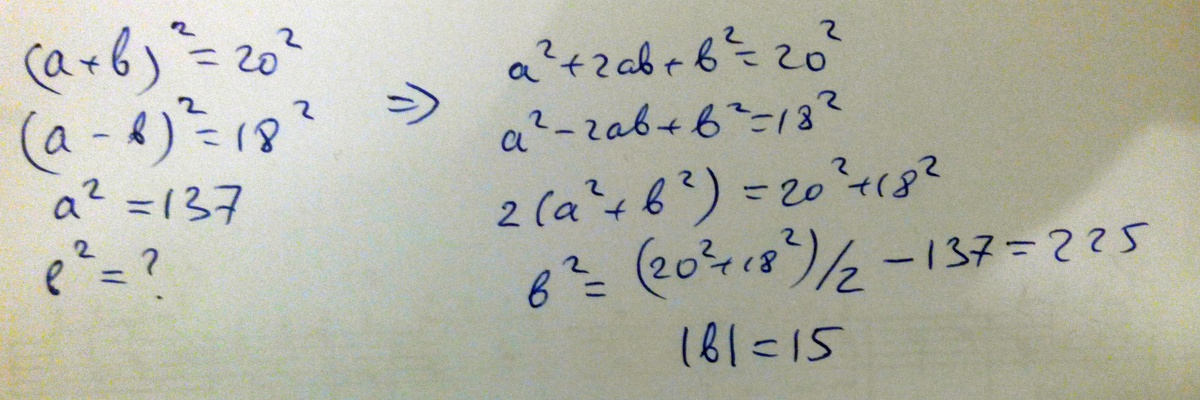
Ответ дал:
0
2)
Модуль суммы двух векторов вычисляется, используя теорему косинусов:
|a + b|² = |a|² + |b|² + 2|a||b|cos(a,b), где cos(a,b) — косинус угла между векторами a и b.
Аналогично и разность двух векторов:
|a - b|² = |a|² + |b|² - 2|a||b|cos(a,b).
Используем известные данные, обозначив разность за х:,
30² = 11² + 23² + 2|a||b|cos(a,b)
х² = 11² + 23² - 2|a||b|cos(a,b)
________________________
30² + х² = 2(11² + 23²)
х² = 1300 - 900 = 400.
х = √400 = 20.
Ответ: длина суммы векторов равна 20.
Модуль суммы двух векторов вычисляется, используя теорему косинусов:
|a + b|² = |a|² + |b|² + 2|a||b|cos(a,b), где cos(a,b) — косинус угла между векторами a и b.
Аналогично и разность двух векторов:
|a - b|² = |a|² + |b|² - 2|a||b|cos(a,b).
Используем известные данные, обозначив разность за х:,
30² = 11² + 23² + 2|a||b|cos(a,b)
х² = 11² + 23² - 2|a||b|cos(a,b)
________________________
30² + х² = 2(11² + 23²)
х² = 1300 - 900 = 400.
х = √400 = 20.
Ответ: длина суммы векторов равна 20.
Приложения:
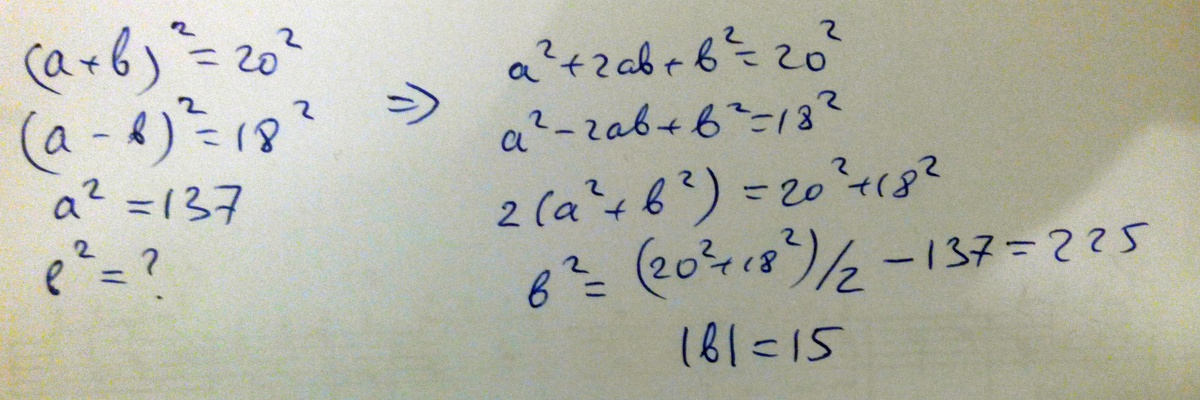
Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад