Ответы
Ответ дал:
0
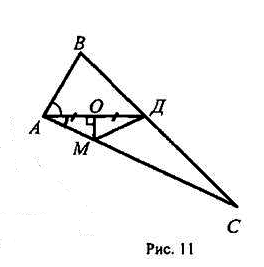
ΔAMD равнобедренный с основанием AD, так как МО - медиана и высота. Значит
∠MAD = ∠MDA
∠MAD = ∠BAD так как AD биссектриса, тогда
∠MDA = ∠BAD, а эти углы - накрест лежащие при пересечении прямых MD и АВ секущей AD, значит
MD║AB
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад