Найдите высоту и боковую сторону равнобокой трапеции ,основания которой равны 5 см и 13 см, а диагонали перпендикулярны боковым сторонам.
Ответы
Ответ дал:
0
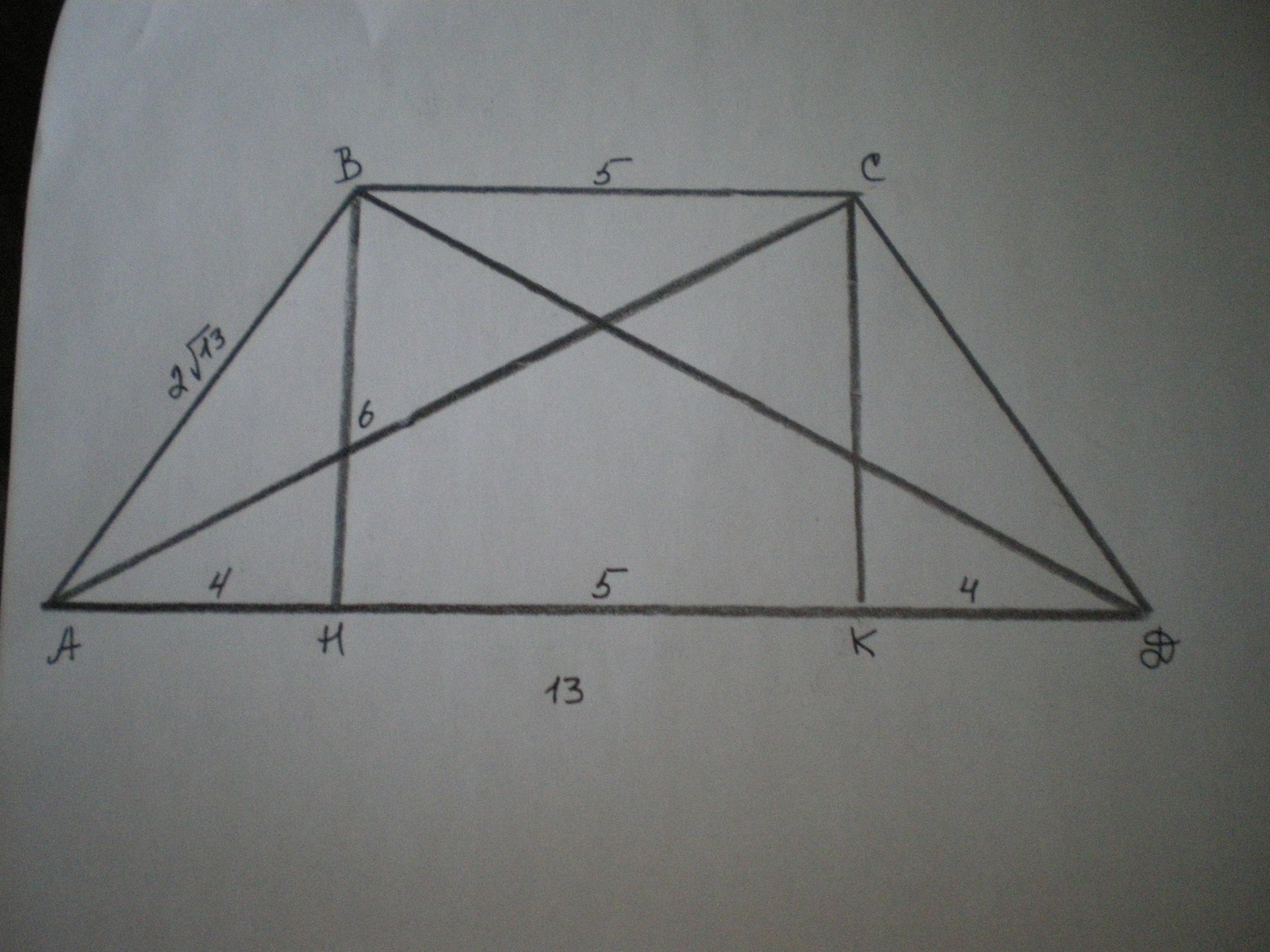
Дано: АВСД - трапеция, АВ=СД, ВС=5 см, АД=13 см. ∠АВД=∠АСД=90°.
Найти АВ и ВН.
Решение: Проведем высоты ВН и СК. Тогда КН=ВС=5 см, АН=КД=(13-5):2=4 см.
Рассмотрим ΔАВД - прямоугольный. По свойству высоты прямоугольного треугольника, проведенной к гипотенузе, ВН²=АН*ДН. ДН=КН+КД=5+4=9 см. ВН²=4*9=36; ВН=6 см.
Рассмотрим ΔАВН - прямоугольный. По теореме Пифагора АВ=√(АН²+ВН²)=√(16+36)=√52=2√13 см.
Ответ: 6 см; 2√13 см.
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад