Здравствуйте ! Помогите , пожалуйста , с геометрией ... Нужно решить задачу на доказательство по теме "Подобия треугольников" ...
Задача: докажите , что отношение соответствующих медиан , подобных треугольников равно коэффициенту подобия .
Большое спасибо за помощь и внимание !!!
Ответы
Ответ дал:
0
Здесь нужно рассмотреть малые треугольники, получившиеся при проведении медиан. Они подобны по второму признаку подобия.
Приложения:
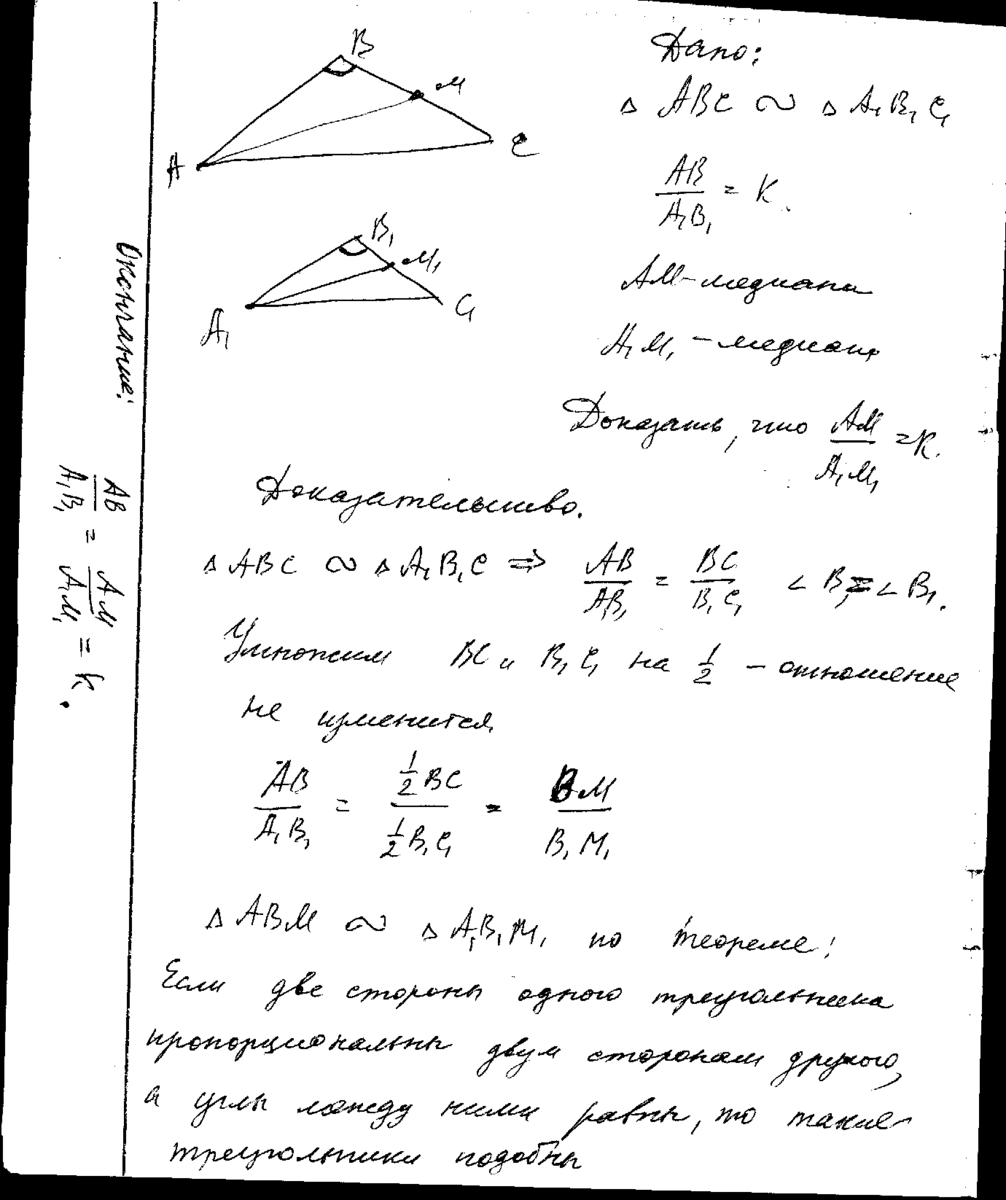
Ответ дал:
0
Спасибо Вам огромное !!!
Ответ дал:
0
Допустим ,что ΔABC ~ ΔA₁B₁C₁ (∠A=∠A₁ ;∠B=∠B₁;∠C=∠C₁) и пусть
AM и A₁M₁ медианы этих треугольников.
ΔABC ~ ΔA₁B₁C₁ ⇒k =AB/A₁B₁ =BC/B₁C₁ ⇒k =AB/A₁B₁ =(BC/2) / (B₁C₁/2), но
BC/2=BM ; B₁C₁/2 =B₁M₁Следовательно k =AB/A₁B₁ =BM / B₁M₁.
Значит ΔABM ~ ΔA₁B₁M₁ (∠B=∠B₁ и стороны этих углов пропорциональны_второй признак подобия треугольников) ,поэтому
k= AB/A₁B₁= AM/A₁M₁.
AM и A₁M₁ медианы этих треугольников.
ΔABC ~ ΔA₁B₁C₁ ⇒k =AB/A₁B₁ =BC/B₁C₁ ⇒k =AB/A₁B₁ =(BC/2) / (B₁C₁/2), но
BC/2=BM ; B₁C₁/2 =B₁M₁Следовательно k =AB/A₁B₁ =BM / B₁M₁.
Значит ΔABM ~ ΔA₁B₁M₁ (∠B=∠B₁ и стороны этих углов пропорциональны_второй признак подобия треугольников) ,поэтому
k= AB/A₁B₁= AM/A₁M₁.
Приложения:

Ответ дал:
0
Большое Вам спасибо !!!
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад