Question

Дам 20 баллов!!
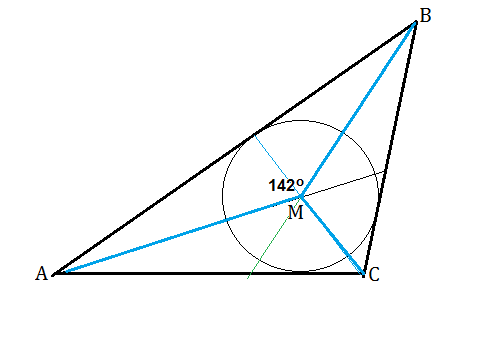
Биссектрисы углов А и В треугольника АВС пересекаются в точке М, причём ∠АМВ=142°. найдите углы АСМ и ВСМ.

Answer 1

В треугольнике АМВ ∠ВАМ +∠МВА=180º -∠АМВ. ∠ВАМ +∠МВА=180º=142º=38º∠ВАМ и ∠МВА - половины углов А и В. Тогда  ∠А+∠В=2*38º=76ªИз ∆ АВС ∠С=180º-76º=104ºБиссектрисы треугольника пересекаются в одной точке.⇒ СМ- биссектриса угла С⇒ ∠АСМ = ∠ВСМ=104º:2=52º