Question

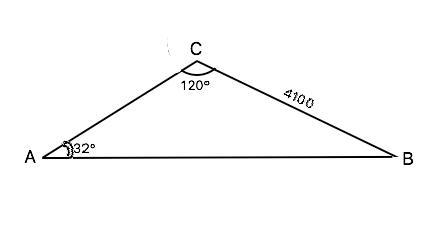
1. Найдите площадь треугольника АВС, если СВ=4100м, угол А=32градуса, угол С=120 градуса. мне бы все точно расписать, очень нужно)

Answer 1

S=0.5*AC*BC*Sin C

По Тереме синусов

AC/Sin b=BC/Sin а

B=180-120-32=28

AC=(4100*Sin(28))/Sin(32)

 

S=0.5*((4100*Sin(28))/Sin(32))*4100*Sin(120)=(4100)^2*Sin(28)*Sin120)/(2*Sin(32))=6449

 

Answer 2

Ответ: 6448728,29 м²

Объяснение: Одна из формул площади треугольника

S=0,5•a•b•sinα. где а и b - стороны треугольника, α – угол между ними.

S=0.5•АС•ВС•sin120°

По т.синусов АС=ВС•sin(B):sin32°

Из суммы углов треугольника угол В=й80°-120°-32°=28° =>

АС=4100•sin28°:sin32°

АС=4100•0.46947:0.52991=3632,36587

S(АВС)=0.5•3632.36587•4100•√3/2=6448728,29 м²