Найдите объем правильной шестиугольной пирамиды,высота которой ровна корень из 3,а боковое ребро - корень из 5
Ответы
Ответ дал:
0
по всем известной формуле , объём пирамиды Vп = 1/3 * Sосн * hп
Sосн - площадь основания
hп - высота пирамиды
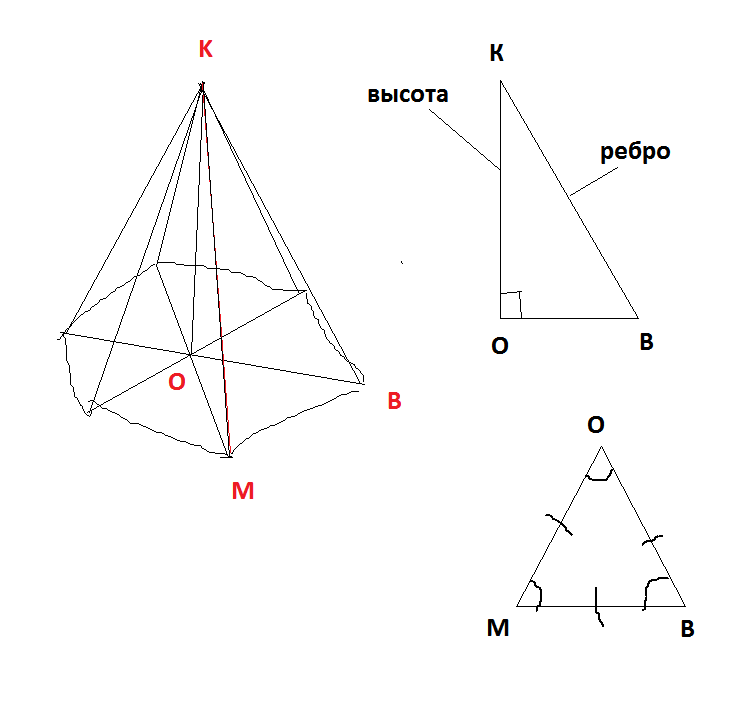
основание состоит из 6 равносторонних треугольников, узнав сторону одного из них мы по формуле Герона или по не менее известной формуле
по двум сторонам и углу между ними,умножив на 6, узнаем площадь основания.
Расмотрим треугольник BKO - прямоугольный(тк KO - высота пирамиды) по формуле пифагора

если считать площадь треуг МОВ по двум сторонам и углу между ними

и

ну и

Sосн - площадь основания
hп - высота пирамиды
основание состоит из 6 равносторонних треугольников, узнав сторону одного из них мы по формуле Герона или по не менее известной формуле
по двум сторонам и углу между ними,умножив на 6, узнаем площадь основания.
Расмотрим треугольник BKO - прямоугольный(тк KO - высота пирамиды) по формуле пифагора
если считать площадь треуг МОВ по двум сторонам и углу между ними
и
ну и
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад