Question

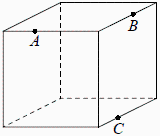
Плоскость, проходящая через три точки A,B иC , разбивает куб на два многогранника. Сколько граней у многогранника, у которого больше рёбер?

Answer 1

если построить плоскость, то будет еще одна точка Д пересечения ее с ребром куба. Эта точка Д будет на ребре идущем из нижнего левого угла влево (недалеко от точки С). В итоге получим плоскость АВСД и многогранник похожий на крыше сарая (двускатную). Визуально видно, что у отсеченной части ребер меньше, чем у оставшейся части. Считаем на ней грани: у куба изначально 6 граней, все они остаются, только добавляется еще плоскость АВСД, значит всего 7 граней.