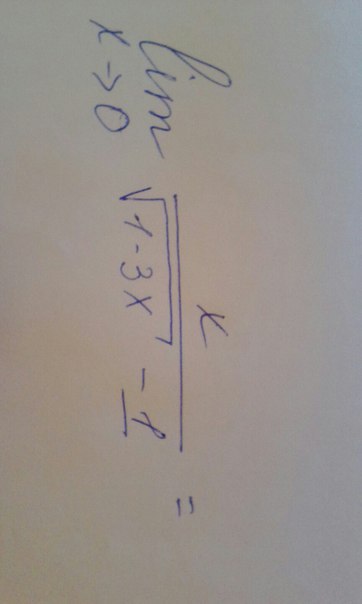Ответы
Ответ дал:
0
lim(x/(√(1-3x)-1))=0/(√(1-3*0)-1)=0/0
x->0
lim([x]/[√(1-3x)-1]=lim([x*(√(1-3x)+1)]/[(√(1-3x)-1)*(√(1-3x)+1)])=
x->0 x->0
=lim([x*(√(1-3x)+1)]/[(√(1-3x))²-1²]=lim([x*(√(1-3x)+1)]/[1-3x-1])=
x->0 x->0
=-lim([√(1-3x)+1]/[3])=-(√(1-3*0)+1)/3=-2/3
x->0
x->0
lim([x]/[√(1-3x)-1]=lim([x*(√(1-3x)+1)]/[(√(1-3x)-1)*(√(1-3x)+1)])=
x->0 x->0
=lim([x*(√(1-3x)+1)]/[(√(1-3x))²-1²]=lim([x*(√(1-3x)+1)]/[1-3x-1])=
x->0 x->0
=-lim([√(1-3x)+1]/[3])=-(√(1-3*0)+1)/3=-2/3
x->0
Приложения:
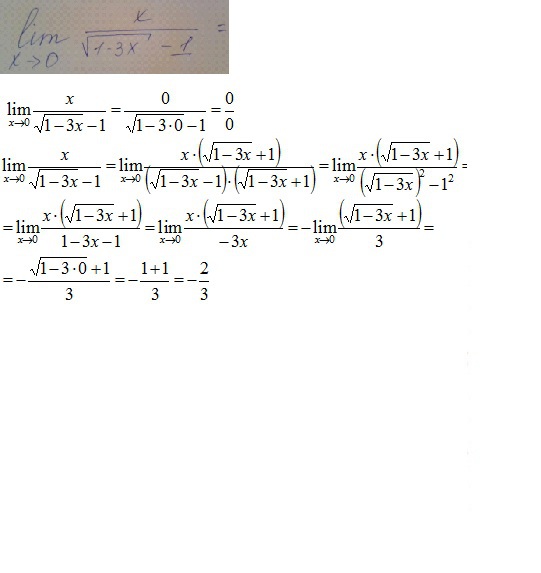
Ответ дал:
0
ааа, все все, просто комментарий не прочитала)))
Ответ дал:
0
сделала "печатный вариант"
Ответ дал:
0
и где он?
Ответ дал:
0
уже в принципе уже не нужно, я разобралась, спасибо)))
Ответ дал:
0
добавлен в виде картинки
Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад