Ответы
Ответ дал:
0
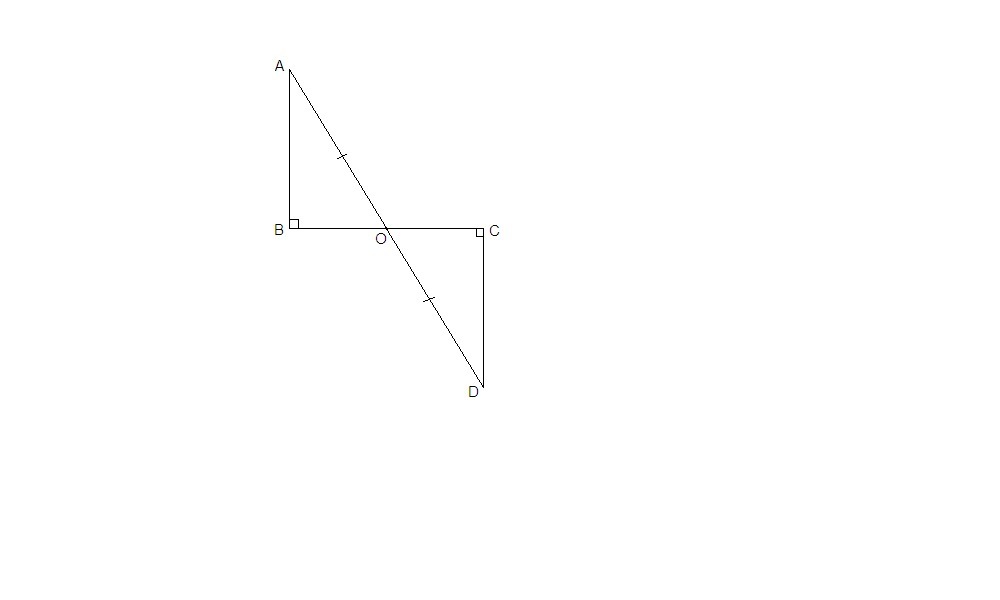
AB║CD как два перпендикуляра к одной прямой (АВ⊥ВС и CD⊥BC), значит
∠ВАО = ∠CDO как накрест лежащие при пересечении параллельных прямых АВ и CD секущей AD.
АО = OD по условию,
∠АОВ = ∠DOC как вертикальные, ⇒
ΔАОВ = ΔDOC по стороне и двум прилежащим к ней углам.
Из равенства треугольников следует, что
∠ВАО = ∠CDO = 38°.
∠ВАО = ∠CDO как накрест лежащие при пересечении параллельных прямых АВ и CD секущей AD.
АО = OD по условию,
∠АОВ = ∠DOC как вертикальные, ⇒
ΔАОВ = ΔDOC по стороне и двум прилежащим к ней углам.
Из равенства треугольников следует, что
∠ВАО = ∠CDO = 38°.
Приложения:
Вас заинтересует
7 лет назад
10 лет назад
10 лет назад
10 лет назад