найдите площадь правильного шестиугольника если площадь кругового сектора соответствующего центральному углу шестиугольника равна 4п
Ответы
Ответ дал:
0
Центральный угол шестиугольника равен:
α = 360° / 6 = 60°
Площадь сектора:
4π = πR² · 60° / 360°
4 = R² / 6
R² = 24
Сторона правильного шестиугольника равна радиусу описанной окружности:
а = R = √24
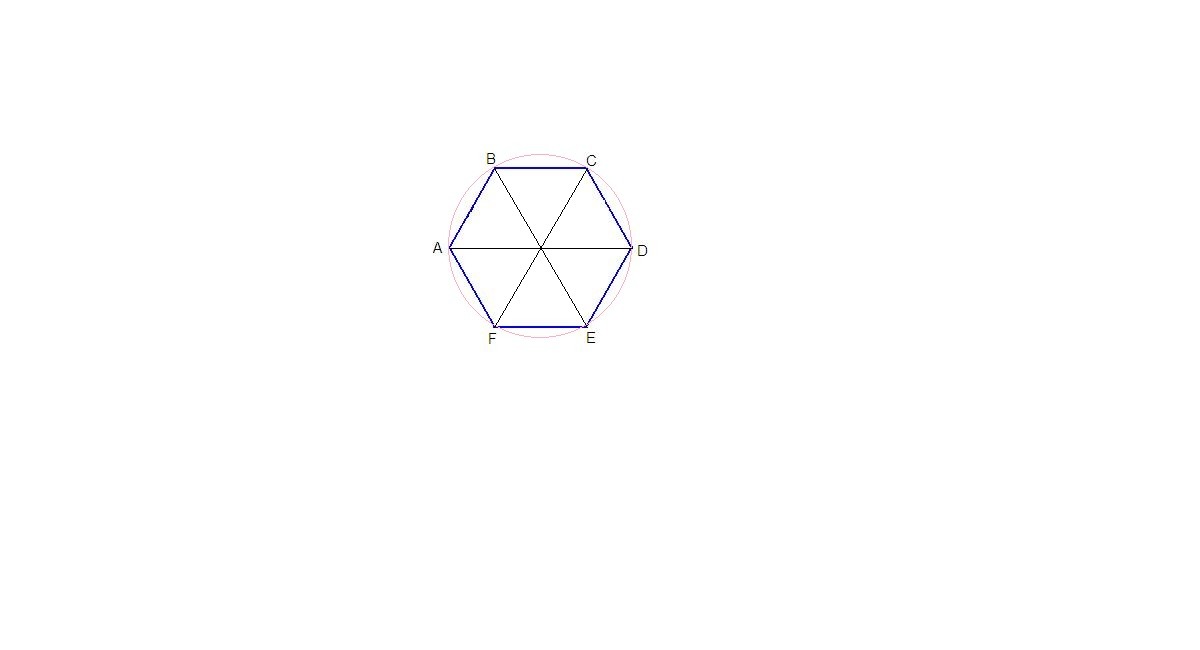
Треугольники, на которые диагонали разбивают шестиугольник, правильные. Площадь одного такого треугольника:
S = a²√3 / 4 = 24√3/4 = 6√3
Тогда площадь шестиугольника:
S = 6 · 6√3 = 36√3 кв. ед.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад