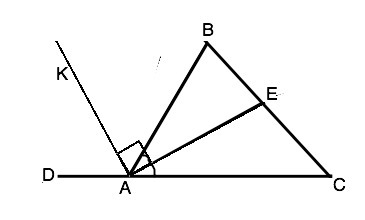
Отрезок АЕ-биссектриса угла А треугольника АВС. Луч АК перпендикулярен АЕ. Докажите, что луч АК-биссектриса внешнего угла треугольника при вершине А.
Ответы
Ответ дал:
0
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.⇒ Из суммы углов треугольника ∠BAD=∠B+∠C=180°-∠A. По условию ∠КАЕ=90°. ⇒ ∠КАВ=90°-∠ВАЕ=90°- 0,5∠А. Угол КАD=180°-∠ВАК=∠180°-∠A-(90°-0,5<A)=90°-0,5∠A. ⇒ углы KAD и КАВ равны, поэтому луч АК - биссектриса внешнего угла ∆ АВС при вершине А.
Приложения:
Вас заинтересует
2 года назад
2 года назад
10 лет назад
10 лет назад