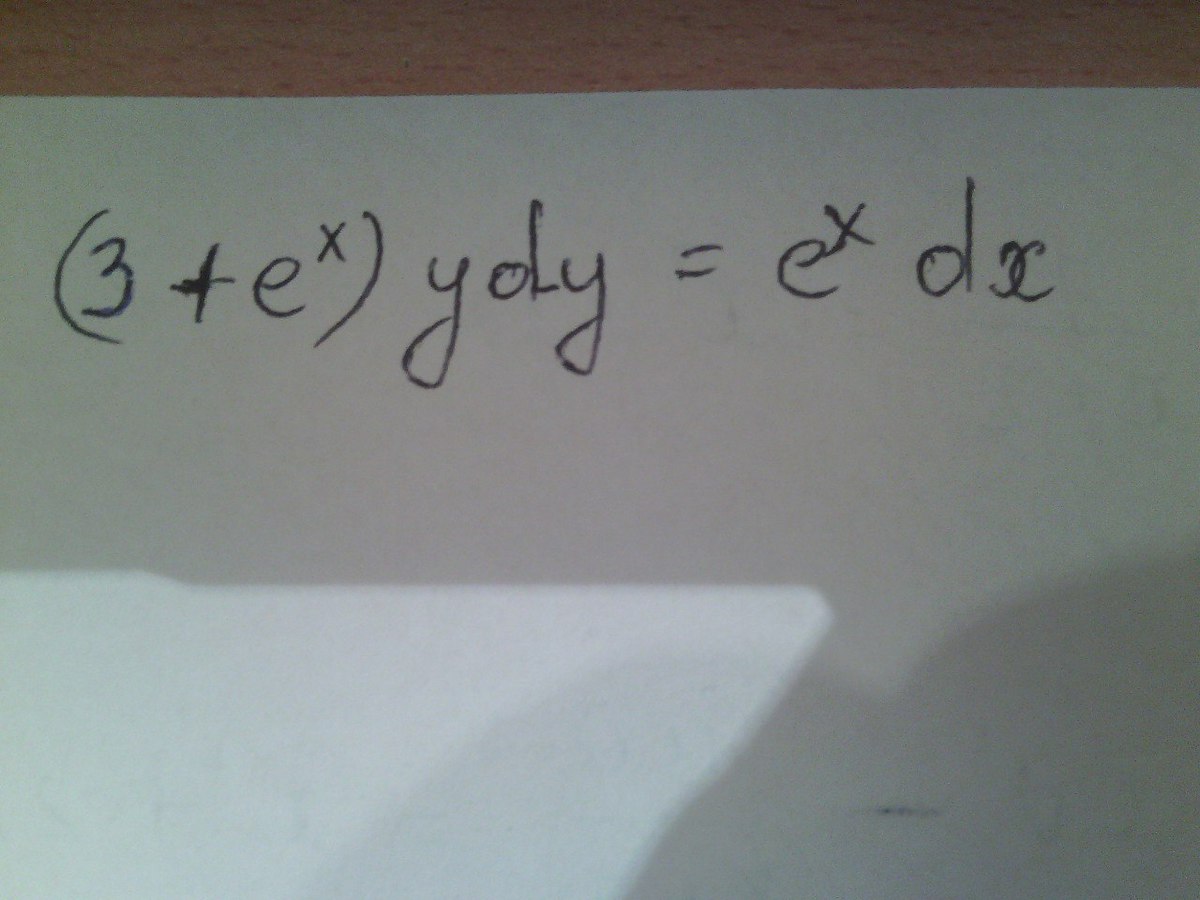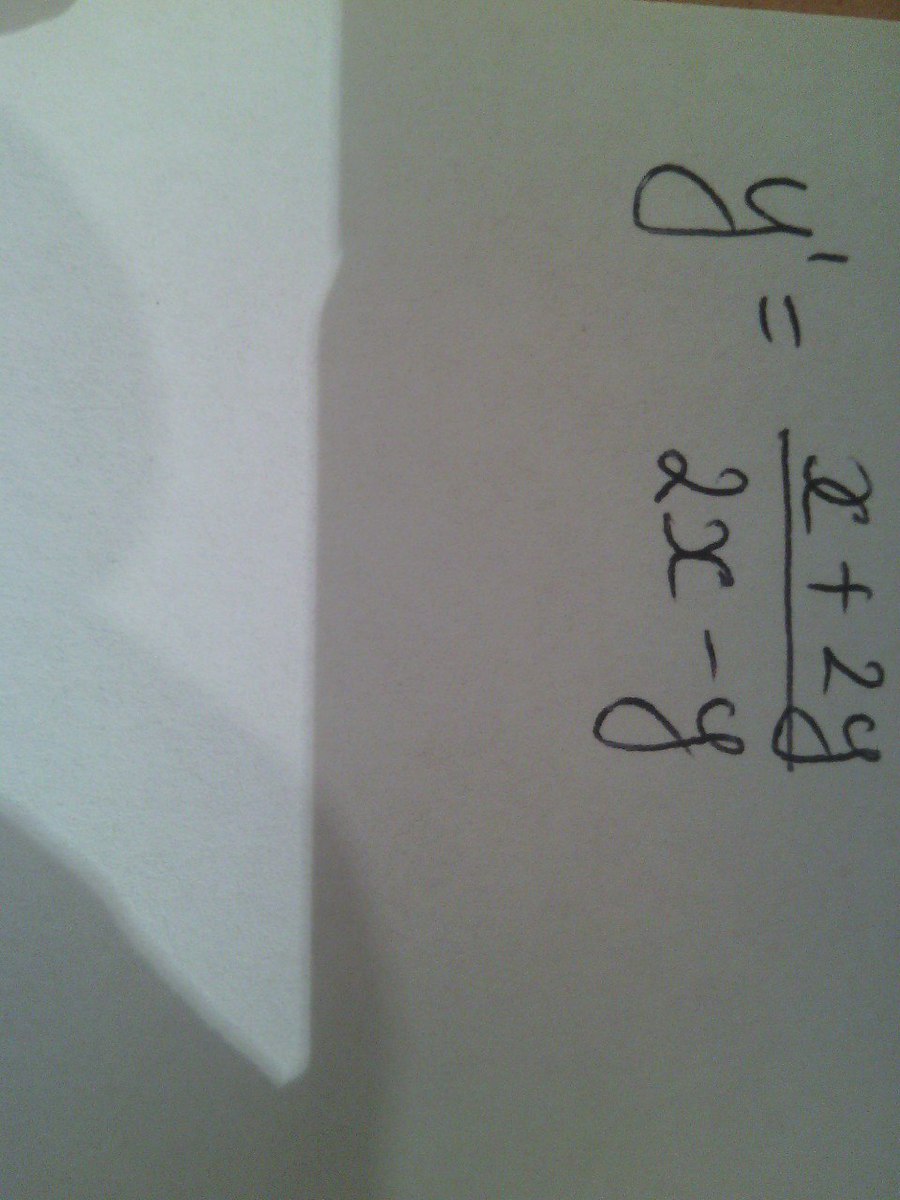Ответы
Ответ дал:
0
Задания даны без начальных условий. А значит, получить конкретные решения дифференциальных уравнений – невозможно.
Если не понятно, что такое начальные условия, поясню.
Например, есть дифференциальное уравнение:
 с начальными условиями
с начальными условиями 
Очевидно, множество решений такого дифференциального уравнения, это:

где и
и  – какие-то неопределённые коэффициенты, которые можно определить через начальные условия.
– какие-то неопределённые коэффициенты, которые можно определить через начальные условия.
Во-первых, убедимся,
что общее решение – вообще верно.
– вообще верно.



итак, общее решение действительно верно.
Найдём конкретное решение,
подставив вместо и
и  – начальные условия
– начальные условия 

поскольку косинус – чётная функция, то и тогда:
и тогда:
 откуда:
откуда: 
Окончательно, конкретное решение дифференциального уравнения с данными начальными условиями
с данными начальными условиями 

Теперь о ваших задачах.
З А Д А Ч А . № . 1

Как и всегда, перетаскиваем всё в одну сторону:

Интегрируем:




Более точное решение этого дифференциального уравнения (как и любого другого) может быть дано только при наличии начальных условий.
З А Д А Ч А . № . 2



Переходим к уравнению с компонентом однородного


Раскрываем составной дифференциал
через общее правило





Переменные разделены на основную и однородную. Теперь интегрируем:






или
Более точное решение этого дифференциального уравнения (как и любого другого) может быть дано только при наличии начальных условий.
Если не понятно, что такое начальные условия, поясню.
Например, есть дифференциальное уравнение:
Очевидно, множество решений такого дифференциального уравнения, это:
где
Во-первых, убедимся,
что общее решение
итак, общее решение действительно верно.
Найдём конкретное решение,
подставив вместо
поскольку косинус – чётная функция, то
Окончательно, конкретное решение дифференциального уравнения
Теперь о ваших задачах.
З А Д А Ч А . № . 1
Как и всегда, перетаскиваем всё в одну сторону:
Интегрируем:
Более точное решение этого дифференциального уравнения (как и любого другого) может быть дано только при наличии начальных условий.
З А Д А Ч А . № . 2
Переходим к уравнению с компонентом однородного
Раскрываем составной дифференциал
через общее правило
Переменные разделены на основную и однородную. Теперь интегрируем:
или
Более точное решение этого дифференциального уравнения (как и любого другого) может быть дано только при наличии начальных условий.
Ответ дал:
0
Да. Таки вот. По поводу начальных условий. В общих решениях ваших заданий (в последних строчках каждой задачи) присутствуют неопределённые величины: R и K. Это какие-то константы, которые можно было бы найти только при задании начальных условий. На всякий случай, замечу, что в таких общих решениях ваших заданий, константа K > 0, а константа R – любое вещественное число, фиксированное в каждом конкретном (частном) решении.
Ответ дал:
0
Х-1+1=3
Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад