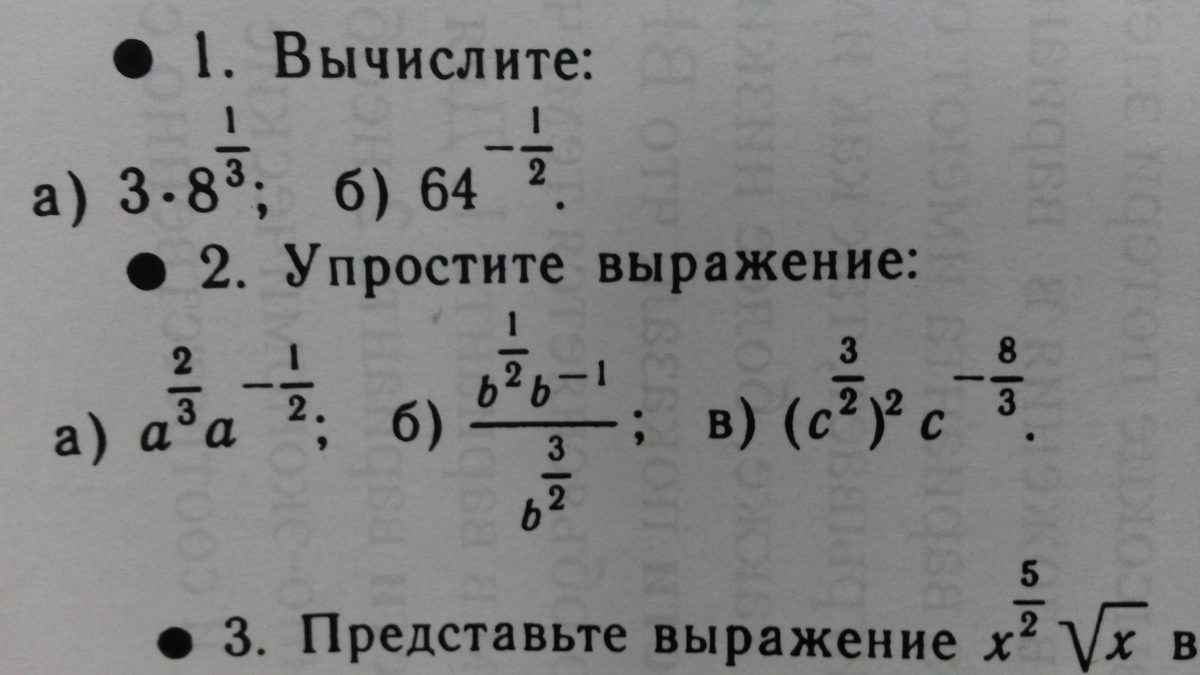Ответы
Ответ дал:
0
1. a) 3*2^(3*1/3)=3*2=6
b) 64^(-1/2)=1/64^(1/2)=
=1/8^(2*1/2)=1/8
2. a) a^2/3 :a^1/2=a^1/6
b) (b^1/2 * b^3/2)/b=b^2/2/b=1
v) c^9/4: c^8/3=c^27/c^32=
=1/c^5
значок ^ обозначает в степени.
1/x^(-1)=x^1, x^(-1)=1/x^1
b) 64^(-1/2)=1/64^(1/2)=
=1/8^(2*1/2)=1/8
2. a) a^2/3 :a^1/2=a^1/6
b) (b^1/2 * b^3/2)/b=b^2/2/b=1
v) c^9/4: c^8/3=c^27/c^32=
=1/c^5
значок ^ обозначает в степени.
1/x^(-1)=x^1, x^(-1)=1/x^1
Ответ дал:
0
Частное двух степеней с одинаковыми основаниями равно выражению, где основание то же самое, а показатель есть разность показателей исходных множителей. Возведение степени числа в степень равно выражению, в котором основание — это то же самое число, а показатель — это произведение двух степеней.
Ответ дал:
0
Сооветственно всё второе задание - не верно
Ответ дал:
0
перечитайте еще и с минусовыми степенями, то что скопировали относится к обычным степеням
Ответ дал:
0
Согласна с первым из второго, a^(1/6), моя ошибка, но другие у меня точно правильны.
Ответ дал:
0
Степень с целым показателем
I. Определение. (- n)-й степенью (n – натуральное) числа а, не равного нулю, считается число, обратное n-й степени числа а:

Примеры. Вычислить:

Решение.

II. Следующая формула позволяет заменить обыкновенную дробь с отрицательным показателем на обратную ей дробь с положительным показателем:

I. Определение. (- n)-й степенью (n – натуральное) числа а, не равного нулю, считается число, обратное n-й степени числа а:

Примеры. Вычислить:

Решение.

II. Следующая формула позволяет заменить обыкновенную дробь с отрицательным показателем на обратную ей дробь с положительным показателем:

Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад