Синусы двух острых углов треугольника равны соответственно 7/25 и 4/5. Найти косинус третьего угла треугольника.
Ответы
Ответ дал:
0
смотрите файл.....................................................
Приложения:
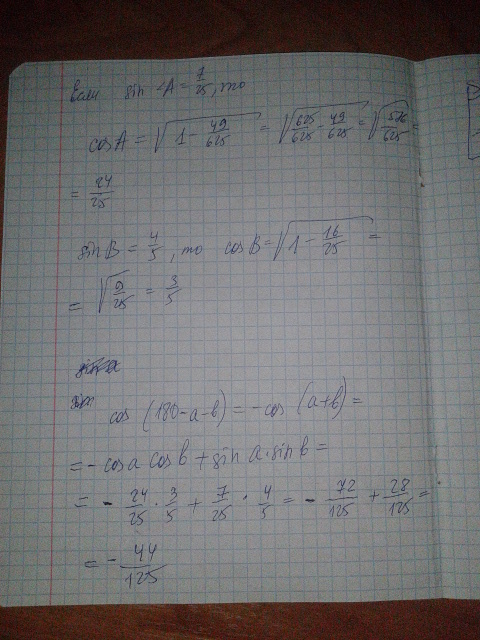
Ответ дал:
0
Нигде не уточнено, что косинус угла треугольника (который, вообще говоря, может быть и тупым) может быть и отрицательным, и что именно на том основании, что углы острые, мы выбираем знак + для косинусов.
Ответ дал:
0
Косинус третьего угла треугольника равен косинусу суммы двух других углов, взятому с противоположным знаком (следствие из тождества cos(a+b) = cosa*cosb - sina*sinb
Если sina = 7/25, cosa = = 24/25,
= 24/25,
cosb = 3/5, cos(a+b) = 24/25*3/5 - 7/25*4/5 = 44/125.
Таким образом, косинус третьего угла треугольника равен - 44/125
Ответ: - 44/125
Если sina = 7/25, cosa =
cosb = 3/5, cos(a+b) = 24/25*3/5 - 7/25*4/5 = 44/125.
Таким образом, косинус третьего угла треугольника равен - 44/125
Ответ: - 44/125
Приложения:
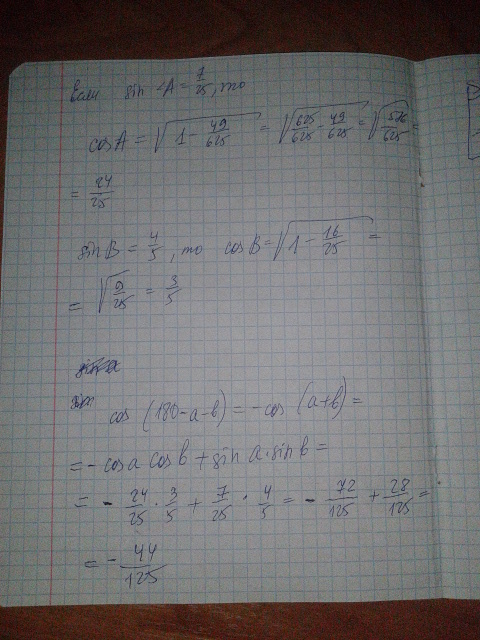
Ответ дал:
0
Нигде не уточнено, что косинус угла треугольника (который, вообще говоря, может быть и тупым) может быть и отрицательным, и что именно на том основании, что углы острые, мы выбираем знак + для косинусов.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад