Question

Найти площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72 кв. дм.
9 класс. Прошу отвечать пользователей, хорошо разбирающихся в геометрии. Пожалуйста, подробное решение или объяснение, чтобы понять...

Answer 1

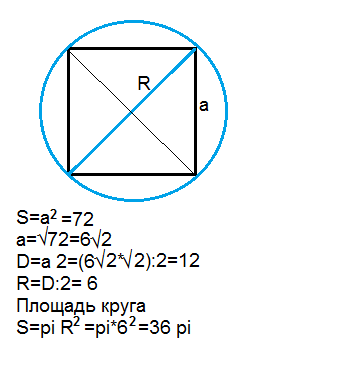
Квадрат вписанный, ⇒ окружность вокруг него - описанная. 
 Радиус описанной вокруг квадрата окружности равен половине диаметра этого квадрата. 
Площадь квадрата равна произведению его сторон или половине произведения его диагоналей: 
S= D*D:2
D²=144
D=√144=12 дм
R=D:2=6 дм
Площадь круга равна πR²
S=π*6²=36π дм²

Answer 2

Большое спасибо!