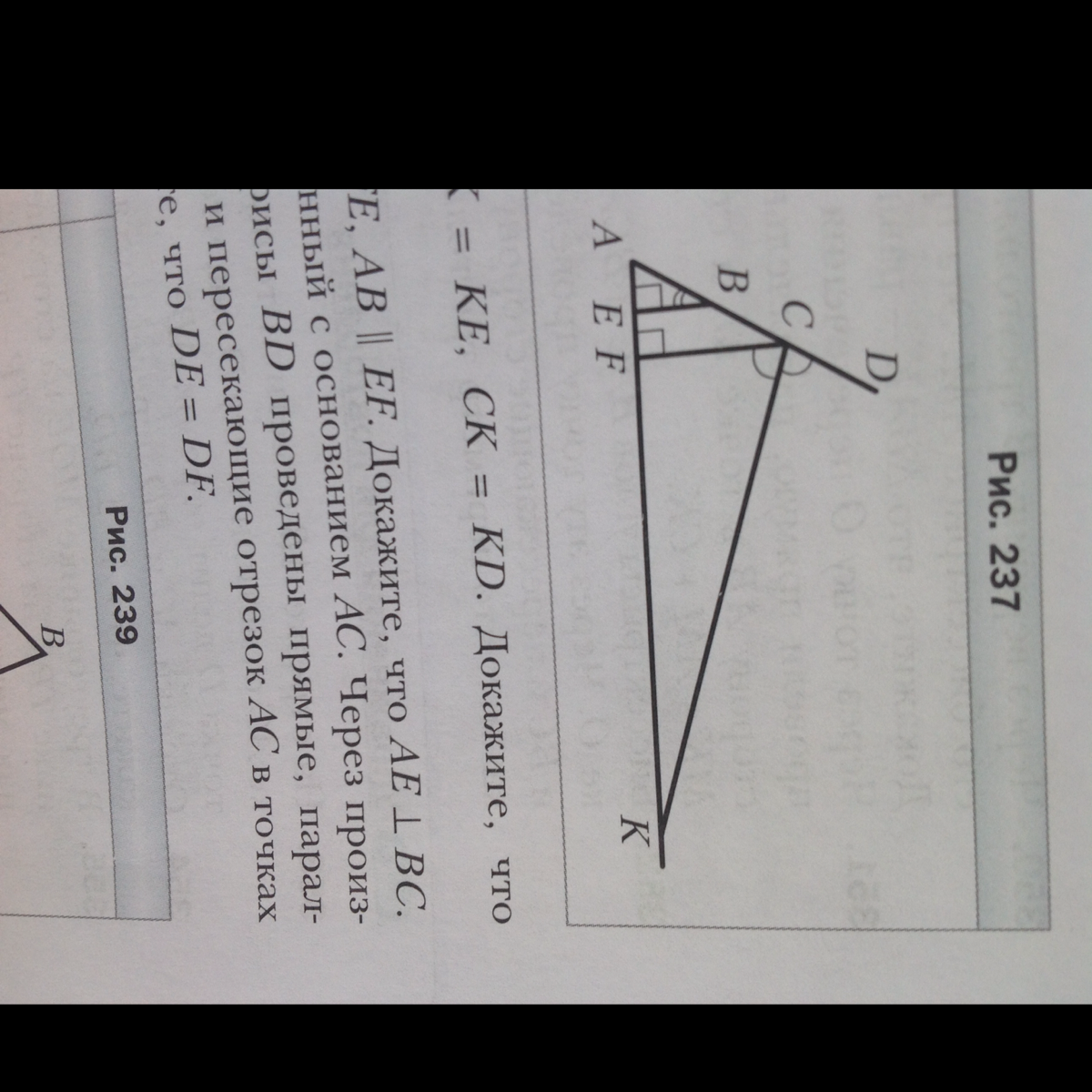
На рисунке 237 ВЕ перпендикулярна АК, CF перпендикулярна АК, СК-биссектриса угла FCD, угол ABE=32 градуса. Наудите угол АСК
Приложения:
Ответы
Ответ дал:
0
ВЕ║CF как два перпендикуляра к одной прямой.
∠ACF = ∠ABE = 32° как соответственные при пересечении параллельных прямых ВЕ и CF секущей АС.
∠DCF = 180° - ∠ACF = 180° - 32° = 148° по свойству смежных углов
∠KCF = ∠DCF/2 = 148°/2 = 74° так как СК биссектриса.
∠АСК = ∠ACF + ∠KCF = 32° + 74° = 106°
∠ACF = ∠ABE = 32° как соответственные при пересечении параллельных прямых ВЕ и CF секущей АС.
∠DCF = 180° - ∠ACF = 180° - 32° = 148° по свойству смежных углов
∠KCF = ∠DCF/2 = 148°/2 = 74° так как СК биссектриса.
∠АСК = ∠ACF + ∠KCF = 32° + 74° = 106°
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад