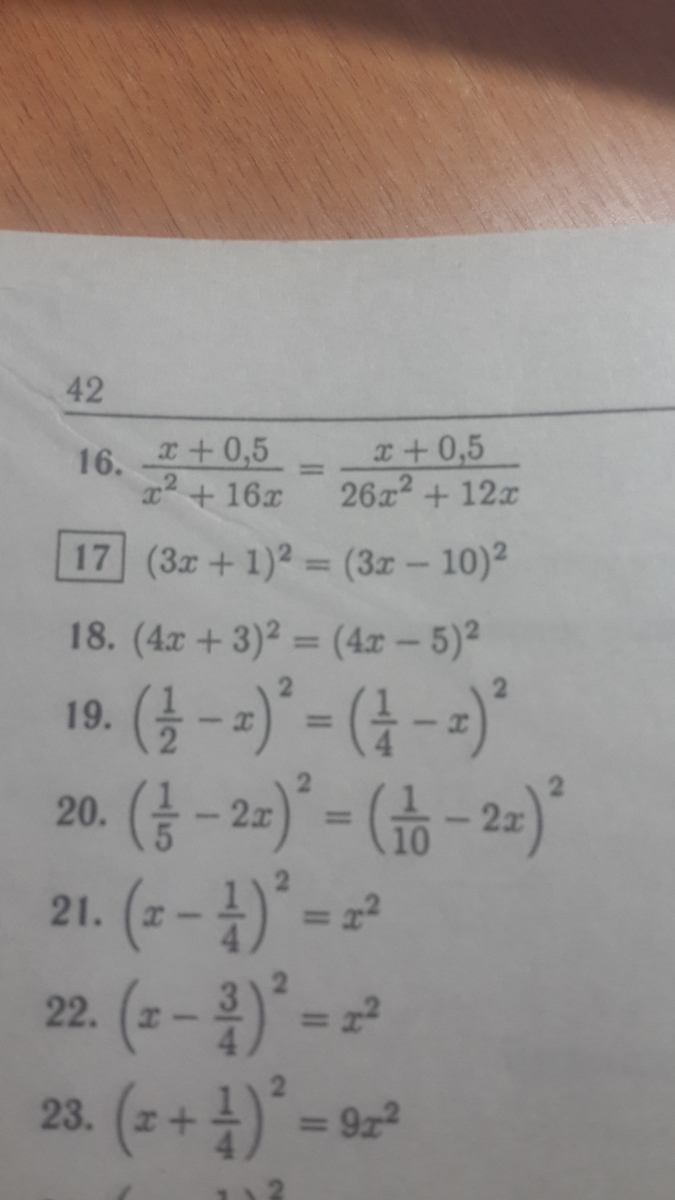Ответы
Ответ дал:
0
определим область допустимых значений ОДЗ:
х²+16х≠0; х(х+16)≠0 х≠0 и х≠-16
26х²+12х≠0; 2х(13х+6)≠0 х≠0 и х≠-6/13
В уравнении числители равны, значит должны быть равны знаменатели
х²+16х=26х²+12х
26х²-х²+12х-16х=0
25х²-4х=0
х(25х-4)=0
х=0 - не подходит, так как не входит в ОДЗ
25х-4=0
25х=4
х=4/25
х=0,16
рассмотрим случай, когда числитель равен нулю
х+0,5=0
х=-0,5
Ответ: -0,5; 0,16
х²+16х≠0; х(х+16)≠0 х≠0 и х≠-16
26х²+12х≠0; 2х(13х+6)≠0 х≠0 и х≠-6/13
В уравнении числители равны, значит должны быть равны знаменатели
х²+16х=26х²+12х
26х²-х²+12х-16х=0
25х²-4х=0
х(25х-4)=0
х=0 - не подходит, так как не входит в ОДЗ
25х-4=0
25х=4
х=4/25
х=0,16
рассмотрим случай, когда числитель равен нулю
х+0,5=0
х=-0,5
Ответ: -0,5; 0,16
Ответ дал:
0
А если числитель равен 0?
Ответ дал:
0
Точно! Спасибо!
Ответ дал:
0
ОДЗ:
1) x^2+16x=x(x+16) не равно 0, значит х1 не равен 0, х2 не равен -16
2) 26x^2+12x=2x(13x+6) х не равен 0 и х не равен -6/13
Решение:
(x+0,5)(26x^2+12x)=(x+0,5)(x^2+16x)
(x+0,5)(26x^2+12x)-(x+0,5)(x^2+16x)=0
(x+0,5)(26x^2+12x-x^2-16x)=0
x1=-1/2
25x^2-4x=0
x(25x-4)=0
x2=0 не проходит по ОДЗ
25х=4
х3=0,16
Ответ: x1=-1/2 x2=0,16
1) x^2+16x=x(x+16) не равно 0, значит х1 не равен 0, х2 не равен -16
2) 26x^2+12x=2x(13x+6) х не равен 0 и х не равен -6/13
Решение:
(x+0,5)(26x^2+12x)=(x+0,5)(x^2+16x)
(x+0,5)(26x^2+12x)-(x+0,5)(x^2+16x)=0
(x+0,5)(26x^2+12x-x^2-16x)=0
x1=-1/2
25x^2-4x=0
x(25x-4)=0
x2=0 не проходит по ОДЗ
25х=4
х3=0,16
Ответ: x1=-1/2 x2=0,16
Вас заинтересует
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад