Question

очень срочно!!!помогите!!!
найти точку максимума функции у=х^3-27х^2+11
подробно.

Answer 1

Чтобы найти точки экстремума функции надо найти производную функции и приравнять её нулю.

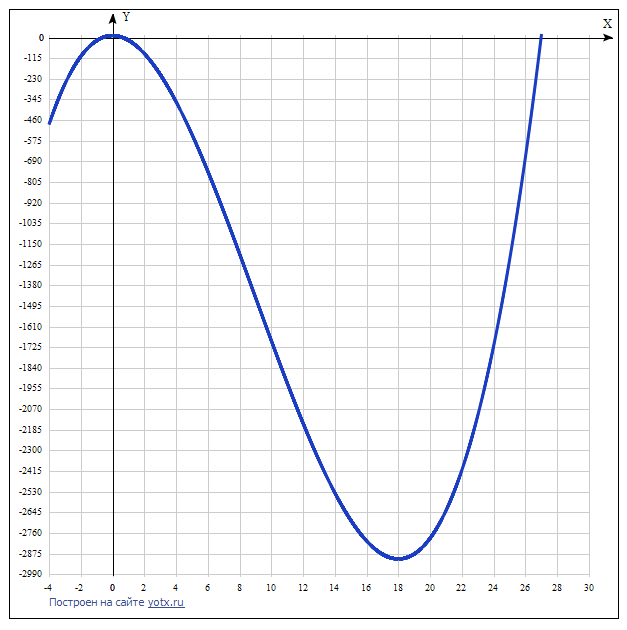
    у =  х^3 - 27х^2 + 11.
    y ' = 3x² - 54x.
    3x² - 54x = 0.
    3x(x - 18) = 0.
Отсюда получаем 2 точки экстремума:
х = 0.
х = 18.

Определение минимума и максимума:
y ' = 3x² - 54х
х =    -1      1       17      19
y ' =   57   -51     -51      57.
х = 0 это максимум,
х = 18 это минимум.

Answer 2

Для определения минимума и максимума функции надо определить поведение производной вблизи критических точек. Если она переходит с + на -, то это максимум, а если с - на +, то это минимум.

Answer 3

т.е.они оба мин?

Answer 4

Нет. внимательно читай!!!

Answer 5

я не поняла 0 мин а 18 мак?

Answer 6

я не поняла 0 мин а 18 мак?