Question

сумма квадратов 2 положительных последовательных четных чисел больше 202. Найдите наименьшее четное число.

Answer 1

Пусть х - это первое четное число, тогда (х+2) -  это второе число.

Сумма квадратов этих чисел равна x²+(x+2)² и оно больше 202

x²+(x+2)² >202

х²+х²+4х +4 >202

2х²+4х+4-202 >0

2х² + 4х - 198 >0

2х² + 4х - 198 =0

упростим,разделив на 2 каждый член

х²+2х-99=0

Д=4+4*99= 400 больше нуля, два корня

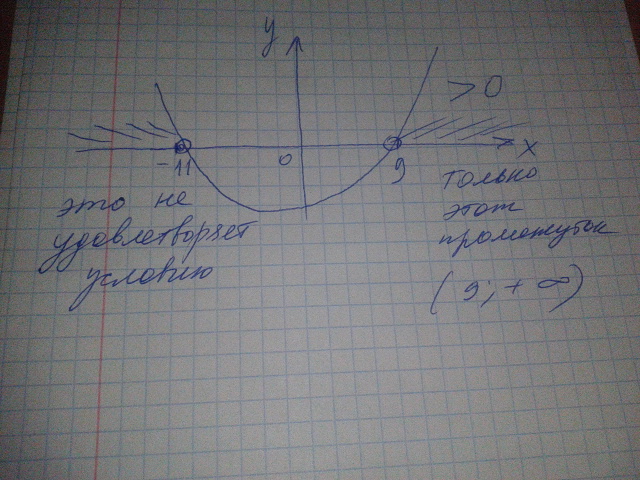
х1= -2+ 20 / 2 = 18 / 2 = 9

х2= -2 -20 / 2  = -22 / 2= -11

Переходим к решению неравенства, это будет промежуток от (9;+ бесконечности)

Наименьшее четное число будет 10