Вычислите интегралы.
Пожалуйста нужно хорошее грамотное решение.
Хотя бы 1 задания на ваш выбор.
Приложения:
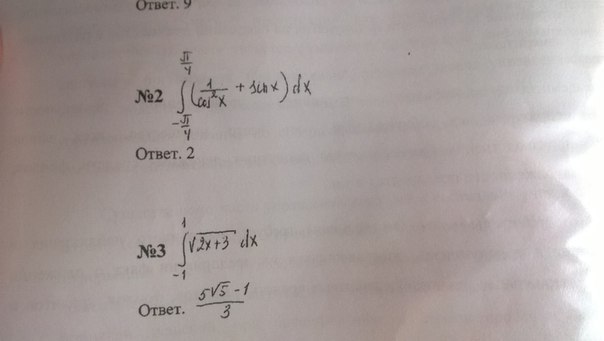
Ответы
Ответ дал:
1
2) = (tgx -Cosx)| в пределах от -π/4 до π/4 =
= (tgπ/4 -Сosπ/4)-(tg(-π/4) - Cos(-π/4))=
=1 -√2/2 +1 +√2/2 = 2
= (tgπ/4 -Сosπ/4)-(tg(-π/4) - Cos(-π/4))=
=1 -√2/2 +1 +√2/2 = 2
Ответ дал:
1
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
7 лет назад
7 лет назад