Question

Сторона равностороннего треугольника равна 63√3дм.

Вычисли:
площадь треугольника;
радиус окружности, вписанной в треугольник;
радиус окружности, описанной около треугольника.

Answer 1

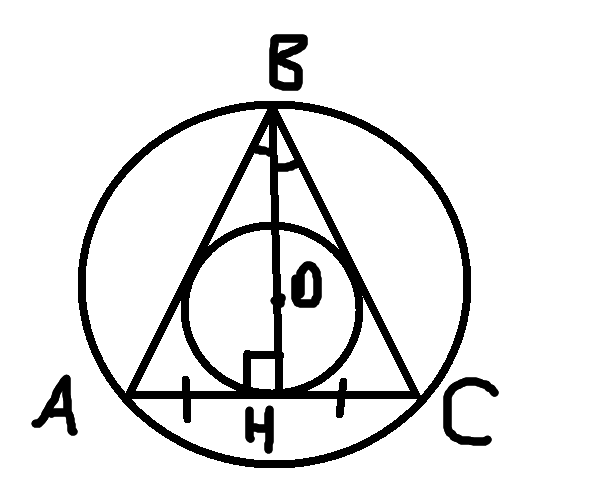
Проведем высоту BH, тогда <AHB=90градуосв, AH=HC=31,5$\sqrt{3}$дм. По теореме Пифагора BH=$\sqrt{11907-2976,75}$=$\sqrt{8930,25}$=94,5дм. Sabc=1/2*94,5дм*63$\sqrt{3}$дм=2976,75$\sqrt{3}$дм^2. r=a/2$\sqrt{3}$=31,5дм.
R=a/$\sqrt{3}$=63дм.
Ответ: Sabc=2976,75$\sqrt{3}$дм^2;  r=31,5дм; R=63дм.