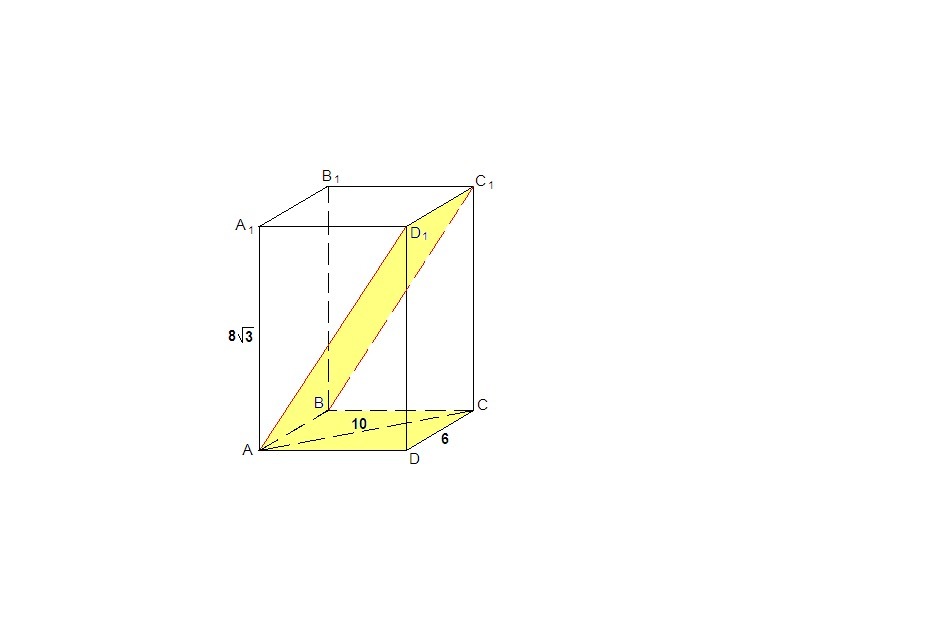
Дан прямоугольный параллелепипед ABCDA1B1C1D1: AC=10 дм, DC=6 дм, AA1=8 корень из 3 дм. Найти градусную меру двугранного угла DABD1
C рисунком
Ответы
Ответ дал:
31
Все грани прямоугольного параллелепипеда - прямоугольники.
Двугранный угол DABD₁ - это угол между плоскостями DAB и ABD₁.
АВ - ребро двугранного угла.
DA⊥AB как стороны квадрата,
DA - проекция наклонной D₁A на плоскость DAB, значит
D₁A⊥АВ по теореме о трех перпендикулярах.
DA⊥AB и D₁A⊥АВ,, значит ∠D₁AD - линейный угол двугранного угла D₁ABD.
ΔADC: ∠ADC = 90°, по теореме Пифагора
AD = √(AC² - CD²) = √(100 - 36) = √64 = 8 дм
ΔD₁AD: ∠D₁DA = 90°, DD₁ = AA₁ = 8√3 дм, AD = 8 дм,
tg∠D₁AD = D₁D / AD = 8√3 / 8 = √3
∠D₁AD = 60°
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад