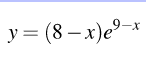Question

Найдите НАИМЕНЬШЕЕ значение функции. На отрезке [3;10]

Answer 1

y=(8-x)*e^(9-x)
y' =- e^(9-x) - (8-x)*e^(9-x)
Находит экстремум функции у(х):
y'=0
 e^(9-x)* (1+8-x) =0
e^(9-x) * (9-x)=0
9-x = 0 ; x = 9 точка экстремума  ∈[3;10]
x>9  y'>0
x<9    y'<0  (в точке х =9 - минимум), моно проверить:
y(10) =(8-10)e^-1= - 2/e≈ -0,7>-1  (e≈2,7) > 
y(9) = - e^0 = - 1
y(8) = 0 > -1
y(7) = e² и т.д., идёт увеличение у при увеличении х
ответ: - 1

Answer 2

не могу понять почему 9 минимальное значение? по моему это max

Answer 3

ну да крен с ним, спасибо за объяснение

Answer 4

нет, минимум, я специально значения у (х) вычислила.

Answer 5

когда проверяете знак производной, смотрите на первую строчку в вычислениях производной

Answer 6

спасибо!