из внешней точке Р проведена касательная к окружности PA=6. Найти радиус окружности, если кратчайшее расстояние от точки P до точек окружности равно 2
Ответы
Ответ дал:
0
Кратчайшее расстояние от точки Р до точек окружности лежит на отрезке, соединяющем точку Р с центром окружности.
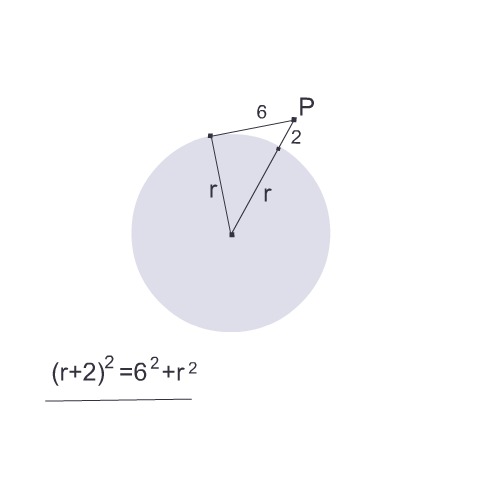
Соединив центр окружности с точкой Р и точкой касания,
получим прямоугольный треугольник с катетами, равными r и 6,
и гипотенузой, равной r+2
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
(r+2)² =6²+r²
r²+4r+4=36+r²
4r=32
r=8
Приложения:
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад