В задаче предполагается, что случайные отклонения контролируемого размера детали, изготов-ленной станком-автоматом, от проектируемого размера подчиняется нормальному закону распре-деления со средним квадратическим отклонением b = 18 (мм) и математическим ожиданием а=0 . Деталь, изготовленная станком-автоматом, считается годной, если отклонение ее контролируемого размера от проектируемого по абсолютной величине не превышает m = 30 (мм). Сколько процентов годных деталей изготовляет станок?
Ответы
Ответ дал:
2
РЕШЕНИЕ
1) Вычисляем отклонение в параметра в СКО
k =m/b = 30/18 = 1 2/3 ~ 1.67
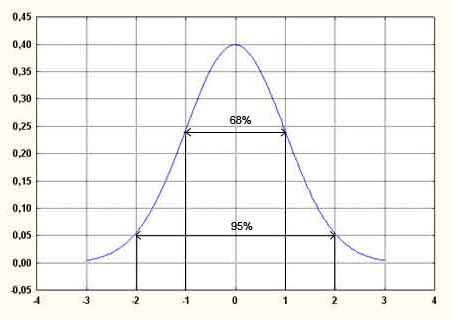
2) По кривой нормального распределения находим процент для к= 1 2/3
Нужны таблицы нормального распределения..
+/-1* СКО = 68% и +-/ 2*СКО = 95%
Нам надо для +/- 1,67*СКО = ?
У меня получилось
р(3+1 2/3) = р(4 2/3= 0,999
р(3- 1 2/3) = р(1 1/3) = 0,15986
И находим разность ~ 0,84 ~ 84% - ОТВЕТ
1) Вычисляем отклонение в параметра в СКО
k =m/b = 30/18 = 1 2/3 ~ 1.67
2) По кривой нормального распределения находим процент для к= 1 2/3
Нужны таблицы нормального распределения..
+/-1* СКО = 68% и +-/ 2*СКО = 95%
Нам надо для +/- 1,67*СКО = ?
У меня получилось
р(3+1 2/3) = р(4 2/3= 0,999
р(3- 1 2/3) = р(1 1/3) = 0,15986
И находим разность ~ 0,84 ~ 84% - ОТВЕТ
Приложения:
xxxeol:
Возможно есть ДРУГОЕ решение
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад