Question

ОГЭ. Математика. 9 класс. 24.
Большее основание равнобедренной трапеции равно 25, а высота относится к
боковой стороне, как 4:5. Найти площадь трапеции, если её диагональ
перпендикулярна боковой стороне.

Answer 1

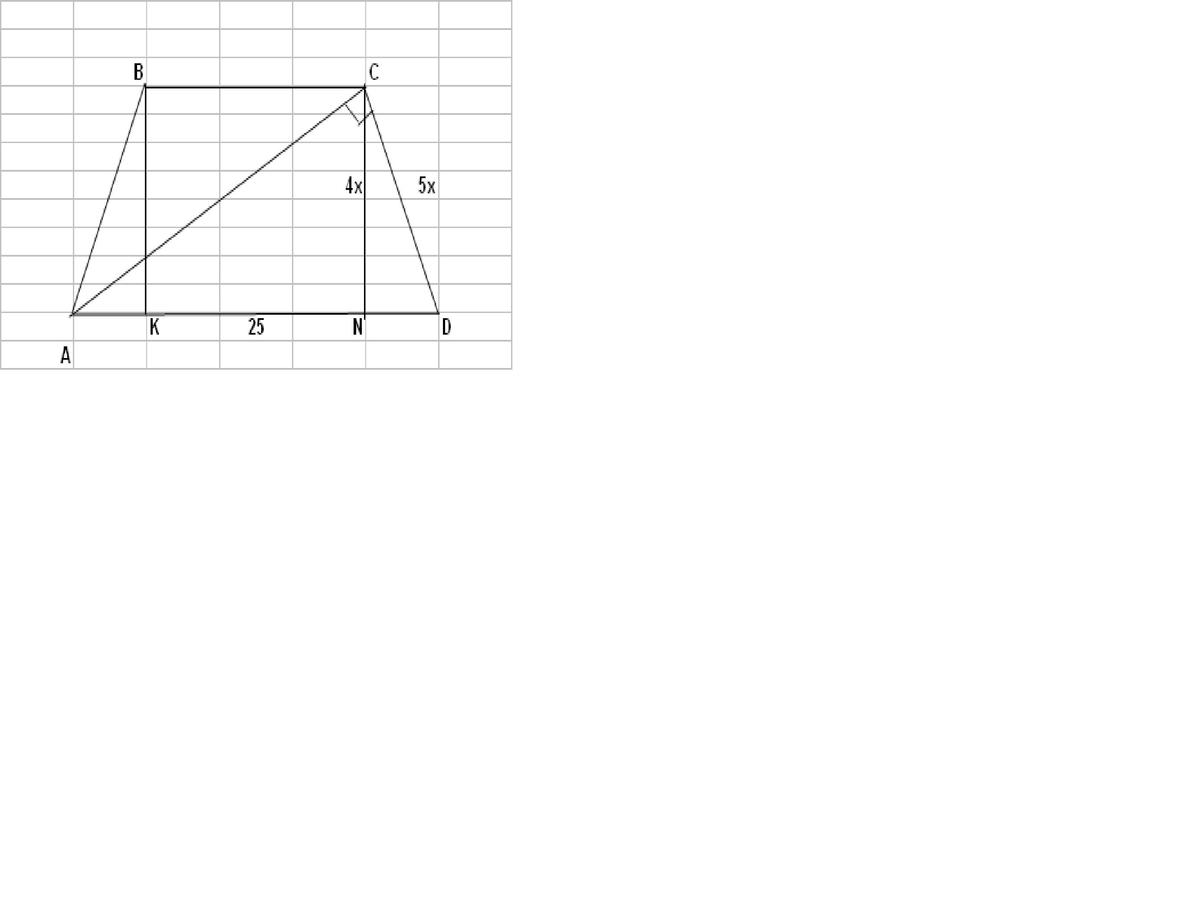
Дано: равнобедренная трапеция ABCD, AB=CD
          CN/CD=4/5 
           AD=25
Найти: S-?

Решение:  

1) рассмотрим ΔCND- прямоугольный т.к. CN- высота,отсюда:

$Sin D= frac{CN}{CD}= frac{4}{5}=0.8 Cos D= sqrt{1-0.64}= sqrt{0.36}=0.6$

2) Рассмотрим Δ ACD- прямоугольный т,к AC⊥CD по условию, отсюда:

$Sin D= frac{AC}{AD} AC=AD*SinD=25*0.8= 20$

$Cos D= frac{CD}{AD} CD= AD*Cos D=25*0.6=15$

т.к. отношение CD/CN=5/4. то CN=12

3) вернемся к Δ CND

$CosD= frac{ND}{CD} ND=CD*CosD=15*0.6=9$

т.к. трапеция равнобедренная то ND=AK=9

Тогда BC= AD-2(ND)=25-2*9=7

4) Таким образом Основания трапеции равны 25 и 7, Высота CN=12
найдем площадь:
$S= frac{1}{2}(AD+BC)*CN= frac{1}{2}(25+7)*12= 192$

Ответ: площадь трапеции 192