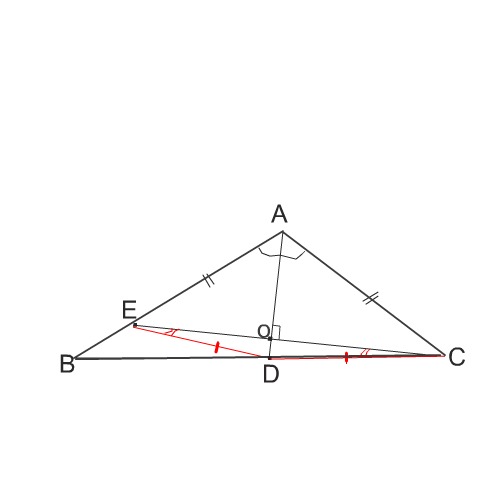
В треугольнике АВС угол В=23,угол С=41.AD-биссектриса, Е такая точка на АВ, что АЕ =АС. Найдите угол BDE
Ответы
Сделаем рисунок.
Соединим точку Е с вершиной С.
Найдем величину угла А
∠А=180°-23°-41°=116°
Так как АЕ=АС, получившийся Δ ЕАС - равнобедренный.
Поскольку в равнобедренном треугольнике биссектриса, проведенная из вершины угла к основанию,является одновременно медианой и высотой, то ЕО=ОС.
∠ЕОА=∠ЕОD=90°
Так как в треугольниках ЕОD и СОD равныстороны ЕО и ОС, ОD -общая, ∠ЕОD=∠СОD=90°
эти треугольники прямоугольные и равны.
Гипотенузы ЕD и DС равны, и треугольник ЕDС - равнобедренный.
∠ ВDЕ равен разности между развернутым углом ВDС и∠ ЕDС
Из треугольника ЕDС
∠ЕDС=180-∠ОЕD-∠ОСD
∠ ОСD=∠АСD-∠АСО
Величину угла АСО найдем из равнобедренного треугольника АЕС.
∠ АЕС=∠АСЕ=(180°-116°):2=32°
∠ОСD=41°-32°=9°
∠ЕDС=180°-9°*2=162°
∠ ВDЕ=180°-162°=18°