Question

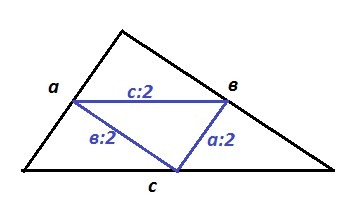
В треугольнике со сторонами а см, в см, с см, (где 2,3 < или равно а < или равно 2,4; 3,2 < или равно в < или равно 3,3; 4,5 < или равно с < или равно 4,6 ) соединены середины сторон. Оцените периметр образовавшегося треугольника.

Answer 1

Чтобы оценить периметр исходного треугольника, нужно сложить заданные неравенства

2,3 ≤ a ≤ 2,4

3,2 ≤ в ≤ 3,3

4,5 ≤ c ≤ 4,6

2,3+3,2+4,5 ≤ a+в+с ≤ 2,4+3,3+4,6

10 ≤ P ≤ 10,3

Соединили середины сторон, то есть провели 3 средние линии треугольника. Каждая средняя линия равна половине стороны, которой параллельна. Значит, периметр образованного треугольника равен половине периметра исходного треугольника

10 ≤ P ≤ 10,3         |   : 2

10:2 ≤ P:2 ≤ 10,3 :2

5 ≤ P₁ ≤ 5,15

Ответ :  периметр полученного треугольника в пределах от 5 см  до  5,15 см   включительно.