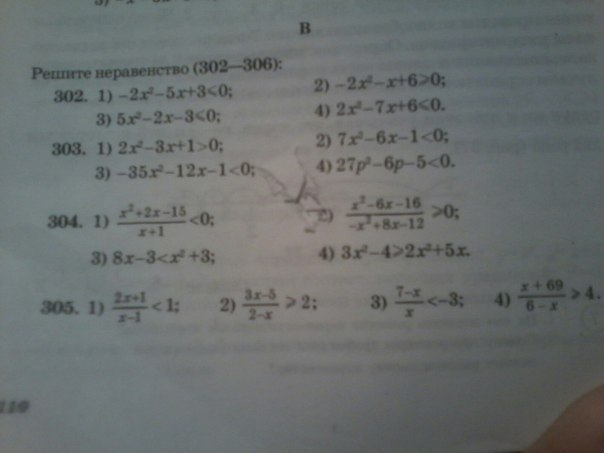Ответы
Ответ дал:
0
305.1) ( 2x+1)/(x-1)<1 ⇔( 2x+1)/(x-1)-1<0 ⇔( 2x+1-x+1)/(x-1)<0 ⇔
(x+2) /(x-1)<0,
1)x+2=0 x=-2, 2) x-1=0 x=1.
+ - +
----------------(-2)---------------------(1)---------------
( x+2) /(x-1)<0 при x∈(-2;1).
305.2)
(3x-5)/(2-x)>2 ⇔ (3x-5)/(2-x)-2 >0 ⇔ [(3x-5)-2(2-x)]/(2-x) >0 ⇔
[3x-5-4+2x]/(2-x) >0 ⇔ [5x-9]/(2-x) >0
1)[5x-9]=0 при x=9/5
2)(2-x)=0 при x=2
-- + -
--------------------------(9/5)--------------(2)-----------------------
[5x-9]/(2-x) >0 при x∈(9/5;2)
(x+2) /(x-1)<0,
1)x+2=0 x=-2, 2) x-1=0 x=1.
+ - +
----------------(-2)---------------------(1)---------------
( x+2) /(x-1)<0 при x∈(-2;1).
305.2)
(3x-5)/(2-x)>2 ⇔ (3x-5)/(2-x)-2 >0 ⇔ [(3x-5)-2(2-x)]/(2-x) >0 ⇔
[3x-5-4+2x]/(2-x) >0 ⇔ [5x-9]/(2-x) >0
1)[5x-9]=0 при x=9/5
2)(2-x)=0 при x=2
-- + -
--------------------------(9/5)--------------(2)-----------------------
[5x-9]/(2-x) >0 при x∈(9/5;2)
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад