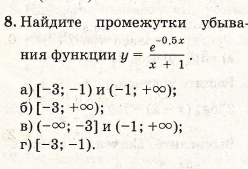Ответы
Ответ дал:
0
1. Находим интервалы возрастания и убывания. Первая производная.
f `(x) = [e^(- 0,5x)] / (x + 1) - [0,5*e^(- 0,5x)] / (x + 1)²
или
f `(x) = (- 0,5x - 1,5)/[(x + 1)² * e^0,5)]
Находим нули функции. Для этого приравниваем производную к нулю
-0.5x - 1.5 = 0
Откуда:
x = - 3
(-∞ ;-3) f'(x) > 0 функция возрастает
(-3; -1) f'(x) < 0 функция убывает
( -1; +∞) f'(x) < 0 функция убывает
В окрестности точки x = - 3 производная функции меняет
знак с (+) на (-). Следовательно, точка x = - 3 - точка максимума.
f `(x) = [e^(- 0,5x)] / (x + 1) - [0,5*e^(- 0,5x)] / (x + 1)²
или
f `(x) = (- 0,5x - 1,5)/[(x + 1)² * e^0,5)]
Находим нули функции. Для этого приравниваем производную к нулю
-0.5x - 1.5 = 0
Откуда:
x = - 3
(-∞ ;-3) f'(x) > 0 функция возрастает
(-3; -1) f'(x) < 0 функция убывает
( -1; +∞) f'(x) < 0 функция убывает
В окрестности точки x = - 3 производная функции меняет
знак с (+) на (-). Следовательно, точка x = - 3 - точка максимума.
Ответ дал:
0
Скажите, пожалуйста. Как вот это получилось "или
f `(x) = (- 0,5x - 1,5)/[(x + 1)² * e^0,5)] "
f `(x) = (- 0,5x - 1,5)/[(x + 1)² * e^0,5)] "
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад