гипотенуза прямоугольного треугольника равна с,а один из острых углов равен a.Найдите объем конуса,образованного при вращении этого треугольника вокруг катета,противолежащего данному углу
Ответы
Ответ дал:
0
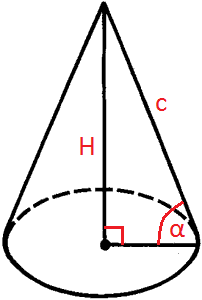
В результате вращения данного треугольника вокруг катета, противолежащему данному углу, получим конус (см рис.), в котором образующая l = c, то есть гипотенуза является образующей; высота H равна катету AB прямоугольного треугольника, то есть  , а радиус конуса равен катету AC
, а радиус конуса равен катету AC  .
.
Найдем объем конуса по формуле:

Ответ:
Найдем объем конуса по формуле:
Ответ:
Приложения:
Вас заинтересует
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад